
【題目】已知用3輛A型車和2輛B型車一次可運貨19噸;用2輛A型車和3輛B型車一次可運貨 21噸.(每輛車每次都滿載貨物)
(1)求1輛A型車和1輛B型車載滿貨物一次分別可以運多少噸?
(2)某貨物中心現有49噸貨物,計劃同時租用A型車和B型車若干輛,一次運完,且恰好每輛車都載滿貨物,請問有哪幾種不同的租車方法.
【答案】(1)1輛A型車一次可以運貨3噸,1輛B型車一次可以運貨5噸;(2)有三種不同的租車方法,①用A型車13輛,B型車2輛;②用A型車8輛,B型車5輛;③用A型車3輛,B型車8輛.
【解析】
(1)設1輛A型車載滿貨物一次可以運貨x噸,1輛B型車載滿貨物一次可以運貨y噸,根據題意列出方程,求解即可;
(2)設用A型車m輛,B型車n輛,由(1)和題意得:3m+5n=49,根據m,n都是正整數,即可求解.
解:(1)設1輛A型車載滿貨物一次可以運貨x噸,1輛B型車載滿貨物一次可以運貨y噸,
根據題意得:![]() ,
,
解得:![]() ,
,
答:1輛A型車一次可以運貨3噸,1輛B型車一次可以運貨5噸;
(2)設用A型車m輛,B型車n輛,
由(1)和題意得:3m+5n=49,
∴m=![]() ,
,
∵m,n都是正整數,
∴![]() 或
或![]() 或
或![]() ,
,
故有三種不同的租車方法,
①用A型車13輛,B型車2輛;
②用A型車8輛,B型車5輛;
③用A型車3輛,B型車8輛.


 超能學典應用題題卡系列答案
超能學典應用題題卡系列答案科目:初中數學 來源: 題型:
【題目】已知二次函數的圖象以 ![]() 為頂點,且過點
為頂點,且過點 ![]() .
.
(1)求該函數的關系式;
(2)求該函數圖象與坐標軸的交點坐標;
(3)將函數圖象向左平移多少個單位,該函數圖象恰好經過原點.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學改革學生的學習模式,變“老師要學生學習”為“學生自主學習”,培養了學生自主學習的能力.小華與小明同學就“你最喜歡哪種學習方式”隨機調查了他們周圍的一些同學,根據收集到的數據繪制了以下兩個不完整的統計圖(如圖).


請根據上面兩個不完整的統計圖回答以下4個問題:
(1)這次抽樣調查中,共調查了_____名學生.
(2)補全條形統計圖中的缺項.
(3)在扇形統計圖中,選擇教師傳授的占_____%,選擇小組合作學習的占_____%.
(4)根據調查結果,估算該校1800名學生中大約有_____人選擇小組合作學習模式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算:
(1)![]() ﹣
﹣![]() +|
+|![]() ﹣3|
﹣3|
(2)x2x4﹣(﹣3x2)3
(3)(m+1)(m﹣3)﹣(m+2)2+(m+2)(m﹣2)
(4)20142﹣2013×2015(用公式計算)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人相約元旦登山,甲、乙兩人距地面的高度y(m)與登山時間x(min)之間的函數圖像如圖所示,根據圖像所提供的信息解答下列問題:
(1)t= min.
(2)若乙提速后,乙登山的上升速度是甲登山的上升速度3倍,
①則甲登山的的上升速度是 m/min;
②請求出甲登山過程中,距地面的高度y(m)與登山時間x(min)之間的函數關系式.
③當甲、乙兩人距地面高度差為70m時,求x的值(直接寫出滿足條件的x值).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線 ![]() 與拋物線
與拋物線 ![]() 交于A、B兩點,點A在x軸上,點B的橫坐標為-8.
交于A、B兩點,點A在x軸上,點B的橫坐標為-8.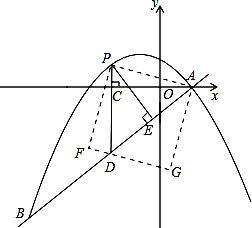
(1)求該拋物線的解析式;
(2)點P是直線AB上方的拋物線上一動點(不與點A、B重合),過點P作x軸的垂線,垂足為C,交直線AB于點D,作PE⊥AB于點E.
①設△PDE的周長為 ![]() ,點P的橫坐標為
,點P的橫坐標為 ![]() ,求
,求 ![]() 關于
關于 ![]() 的函數關系式,并求出
的函數關系式,并求出 ![]() 的最大值;
的最大值;
②連接PA,以PA為邊作圖示一側的正方形APFG.隨著點P的運動,正方形的大小、位置也隨之改變.當頂點F或G恰好落在 ![]() 軸上時,求出對應點P的坐標.
軸上時,求出對應點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】推理填空
如圖,已知AB∥CD,∠A=∠C,試說明∠B=∠D.
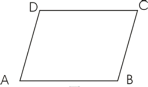
解:∵AB∥CD(已知)
∴∠B+∠C=180°( )
又∵∠A=∠C(已知)
∴∠B+________=180°(等量代換)
∴AD∥BC ( )
∴∠C+∠D=180°( )
又∵∠B+∠C=180°(已證)
∴∠B=∠D ( )
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在“元旦”期間,平價商場對該商場商品進行如下的優惠促銷活動:
打折前一次性購物總金額 | 優惠措施 |
小于等于 400 元 | 不優惠 |
超過 400 元,但不超過 600元 | 按售價打九折 |
超過 600 元 | 其中 600 元部分八折優惠,超過 600 元的部分打六折優惠 |
按上述優惠條件,若小華一次性購買售價為 80 元/件的商品 n 件時,實際付款 504 元, 則 n=_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】以點A為頂點作兩個等腰直角三角形(△ABC,△ADE),如圖1所示放置,使得一直角邊重合,連接BD,CE.

(1)說明BD=CE;
(2)延長BD,交CE于點F,求∠BFC的度數;
(3)若如圖2放置,上面的結論還成立嗎?請簡單說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com