
【題目】復習課中,教師給出關于x的函數y=2kx2-(4k+1)x-k+1(k是實數).教師:請獨立思考,并把探索發現的與該函數有關的結論(性質)寫到黑板上.學生思考后,黑板上出現了一些結論,教師作為活動一員,又補充一些結論,并從中選出如下四條:
①存在函數,其圖象經過(1,0)點;
②存在函數,該函數的函數值y始終隨x的增大而減小;
③函數圖象有可能經過兩個象限;
④若函數有最大值,則最大值必為正數,若函數有最小值,則最小值必為負數.
其中正確的結論有 .
【答案】①②④
【解析】①將(1,0)代入可得:2k-(4k+1)-k+1=0,解得:k=0,此選項正確.
②當k=0時,y=-x+1,該函數的函數值y始終隨x的增大而減小;此選項正確;
③y=-x+1,經過3個象限,此選項錯誤;
④當k=0時,函數無最大、最小值;k≠0時,y最=- ![]() ,當k>0時,有最小值,最小值為負;當k<0時,有最大值,最大值為正;此選項正確.
,當k>0時,有最小值,最小值為負;當k<0時,有最大值,最大值為正;此選項正確.
正確的是①②④.
【考點精析】關于本題考查的一次函數的性質和二次函數圖象以及系數a、b、c的關系,需要了解一般地,一次函數y=kx+b有下列性質:(1)當k>0時,y隨x的增大而增大(2)當k<0時,y隨x的增大而減小;二次函數y=ax2+bx+c中,a、b、c的含義:a表示開口方向:a>0時,拋物線開口向上; a<0時,拋物線開口向下b與對稱軸有關:對稱軸為x=-b/2a;c表示拋物線與y軸的交點坐標:(0,c)才能得出正確答案.


 長江作業本同步練習冊系列答案
長江作業本同步練習冊系列答案科目:初中數學 來源: 題型:
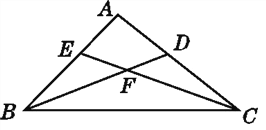
【題目】如圖,以CD為公共邊的三角形是____________;∠EFB是____________的內角;在△BCE中,BE所對的角是____________,∠CBE所對的邊是____________;以∠A為公共角的三角形是____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】環保健康的“共享單車”已成為人們短途出行的一種新方式,一輛新投放市場的單車其先期成本為1050元.如圖是一輛新投放的共享單車其運營收入w1和運營支出w2關于時間m的函數圖象. 
注:一輛單車的盈利=運營收入﹣運營支出﹣先期成本
(1)分別求w1及運營60天后w2關于時間m的函數關系式.
(2)求一輛新投放市場的單車恰好收回先期成本需要運營多少天?
(3)某公司投放市場一批單車,其先期成本不少于2.1萬元但不超過10.5萬元,經過一段時間的市場試運營共盈利3550元,則該公司試運營的天數為天(直接寫出答案).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是二次函數y=ax2+bx+c圖象的一部分,圖象過點A(-3,0),對稱軸為x=-1.給出四個結論:①b2 > 4ac;②2a+b=0;③a-b+c=0;④5a < b.其中正確結論有( )
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 中,
中,![]() ,點
,點![]() 分別是邊
分別是邊![]() 上的點,點
上的點,點![]() 是一動點,令
是一動點,令![]() ,
,![]() ,
,![]() .
.
(1)若點![]() 在線段
在線段![]() 上,如圖①所示,且
上,如圖①所示,且![]() ,則
,則![]() _____
_____![]() ;
;
(2)若點![]() 在邊
在邊![]() 上運動,如圖②所示,則
上運動,如圖②所示,則![]() 、
、![]() 、
、![]() 之間的關系為______;
之間的關系為______;
(3)如圖③,若點![]() 在斜邊
在斜邊![]() 的延長線上運動
的延長線上運動![]() ,請寫出
,請寫出![]() 、
、![]() 、
、![]() 之間的關系式,并說明理由.
之間的關系式,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】興隆商場用36萬元購進A、B兩種品牌的服裝,銷售完后共獲利6萬元,其進價和售價如下表:

該商場購進A、B兩種服裝各多少件?
(2)第二次以原價購進A、B兩種服裝,購進B服裝的件數不變,購進A服裝的件數是第一次的2倍,A種服裝按原價出售,而B種服裝打折銷售;若兩種服裝銷售完畢,要使第二次銷售活動獲利不少于81600元,則B種服裝最低打幾折銷售?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠AOB=120°,OC是∠AOB內部任意一條射線,OD,OE分別是∠AOC,∠BOC的角平分線,下列敘述正確的是( )

A. ∠AOD+∠BOE=60°B. ∠AOD=![]() ∠EOC
∠EOC
C. ∠BOE=2∠CODD. ∠DOE的度數不能確定
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖, 已知A(-4,-1),B(-5,-4),C(-1,-3),△ABC經過平移得到的△A′B′C′,△ABC中任意一點P(x1,y1)平移后的對應點為P′(x1+6,y1+4)。
(1)請在圖中作出△A′B′C′;(2)寫出點A′、B′、C′的坐標.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com