
【題目】如圖,直線y=x+b(b>4)與x軸、y軸分別相交于點A、B,與反比例函數 ![]() 的圖象相交于點C、D(點C在點D的左側),⊙O是以CD長為半徑的圓.CE∥x軸,DE∥y軸,CE、DE相交于點E.
的圖象相交于點C、D(點C在點D的左側),⊙O是以CD長為半徑的圓.CE∥x軸,DE∥y軸,CE、DE相交于點E. 
(1)△CDE是三角形;點C的坐標為 , 點D的坐標為(用含有b的代數式表示);
(2)b為何值時,點E在⊙O上?
(3)隨著b取值逐漸增大,直線y=x+b與⊙O有哪些位置關系?求出相應b的取值范圍.
 一本好題口算題卡系列答案
一本好題口算題卡系列答案科目:初中數學 來源: 題型:
【題目】我們在學完“平移、軸對稱、旋轉”三種圖形的變化后,可以進行進一步研究,請根據示例圖形,完成下表.
圖形的變化 | 示例圖形 | 與對應線段有關的結論 | 與對應點有關的結論 |
平移 |
| AA′=BB′ | |
軸對稱 |
| ||
旋轉 |
| AB=A′B′;對應線段AB和A′B′所在的直線相交所成的角與旋轉角相等或互補. |
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知A,B是反比例函數y= ![]() (k>0,x>0)圖象上的兩點,BC∥x軸,交y軸于點C,動點P從坐標原點O出發,沿O→A→B→C(圖中“→”所示路線)勻速運動,終點為C,過P作PM⊥x軸,垂足為M.設三角形OMP的面積為S,P點運動時間為t,則S關于x的函數圖象大致為( )
(k>0,x>0)圖象上的兩點,BC∥x軸,交y軸于點C,動點P從坐標原點O出發,沿O→A→B→C(圖中“→”所示路線)勻速運動,終點為C,過P作PM⊥x軸,垂足為M.設三角形OMP的面積為S,P點運動時間為t,則S關于x的函數圖象大致為( ) 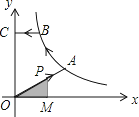
A.
B.
C.
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,點P在AB的延長線上,弦CE交AB于點D.連接OE、AC,且∠P=∠E,∠POE=2∠CAB.
(1)求證:CE⊥AB;
(2)求證:PC是⊙O的切線;
(3)若BD=2OD,PB=9,求⊙O的半徑及tan∠P的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了進一步開展“陽光體育”活動,計劃用2000元購買乒乓球拍,用2800元購買羽毛球拍.已知一副羽毛球拍比一副乒乓球拍貴14元.該校購買的乒乓球拍與羽毛球拍的數量能相同嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是使用測角儀測量一幅壁畫高度的示意圖,已知壁畫AB的底端距離地面的高度BC=1m,在壁畫的正前方點D處測得壁畫底端的俯角∠BDF=30°,且點D距離地面的高度DE=2m,求壁畫AB的高度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 如圖,△ABC中,∠ACB=90°,AB=8cm,D是AB的中點.現將△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,則GH的長等于cm. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1個單位長度的小正方形組成的網格中,△ABC的頂點A、B、C在小正方形的頂點上,將△ABC向下平移4個單位、再向右平移3個單位得到△A1B1C1 , 然后將△A1B1C1繞點A1順時針旋轉90°得到△A1B2C2 . 
(1)在網格中畫出△A1B1C1和△A1B2C2;
(2)計算線段AC在變換到A1C2的過程中掃過區域的面積(重疊部分不重復計算)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ABC=90°,點D在BC的延長線上,且BD=AB,過點B作BE⊥AC,與BD的垂線DE交于點E. 
(1)求證:△ABC≌△BDE;
(2)△BDE可由△ABC旋轉得到,利用尺規作出旋轉中心O(保留作圖痕跡,不寫作法).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com