
【題目】如圖,過點C(1,2)分別作x軸,y軸的平行線,交直線y=-x+6于點A,B,若反比例函數y=![]() (x>0)的圖象與△ABC有公共點,求k的取值范圍.
(x>0)的圖象與△ABC有公共點,求k的取值范圍.

【答案】2≤k≤9
【解析】先求出點A、B的坐標,根據反比例函數系數的幾何意義可知,當反比例函數圖象與△ABC相交于點C時k的取值最小,當與線段AB相交時,k能取到最大值,根據直線y=-x+6,設交點為(x,-x+6)時k值最大,然后列式利用二次函數的最值問題解答即可得解.
∵點C(1,2),BC∥y軸,AC∥x軸,
∴當x=1時,y=-1+6=5,
當y=2時,-x+6=2,解得x=4,
∴點A、B的坐標分別為A(4,2),B(1,5),
根據反比例函數系數的幾何意義,當反比例函數與點C相交時,k=1×2=2最小,
設反比例函數與線段AB相交于點(x,-x+6)時k值最大,
則k=x(-x+6)=-x2+6x=-(x-3)2+9,
∵1≤x≤4,
∴當x=3時,k值最大,
此時交點坐標為(3,3),
因此,k的取值范圍是2≤k≤9.


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案科目:初中數學 來源: 題型:
【題目】已知,如圖,O為正方形對角線的交點,BE平分∠DBC,交DC于點E,延長BC到點F,使CF=CE,連結DF,交BE的延長線于點G,連結OG.
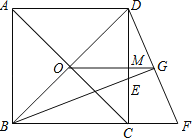
(1)求證:△BCE≌△DCF.
(2)判斷OG與BF有什么關系,證明你的結論.
(3)若DF2=8-4![]() ,求正方形ABCD的面積?
,求正方形ABCD的面積?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某廠倉庫儲存了部分原料,按原計劃每時消耗2 t,可用60 h.由于技術革新,實際生產能力有所提高,即每時消耗的原料量大于計劃消耗的原料量.設現在每時消耗原料x(單位:t),庫存的原料可使用的時間為y(單位:h).
(1)寫出y關于x的函數解析式,并求出自變量的取值范圍;
(2)若恰好經過24 h才有新的原料進廠,為了使機器不停止運轉,則x應控制在什么范圍內?
查看答案和解析>>
科目:初中數學 來源: 題型:
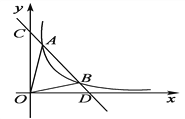
【題目】如圖,一次函數y=kx+b與反比例函數y=![]() (x>0)的圖象交于A(m,6),B(3,n)兩點.
(x>0)的圖象交于A(m,6),B(3,n)兩點.
(1)求一次函數的解析式;
(2)根據圖象直接寫出kx+b-![]() <0時x的取值范圍;
<0時x的取值范圍;
(3)求△AOB的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某運輸隊要運300 t物資到江邊防洪.
(1)運輸時間t(單位:h)與運輸速度v(單位:t/h)之間有怎樣的函數關系式?
(2)運了一半時,接到防洪指揮部命令,剩下的物資要在2 h之內運到江邊,則運輸速度至少為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(中考·安徽)如圖,已知反比例函數y=![]() 與一次函數y=k2x+b的圖象交于A(1,8),B(-4,m).
與一次函數y=k2x+b的圖象交于A(1,8),B(-4,m).

(1)求k1,k2,b的值;
(2)求△AOB的面積;
(3)若M(x1,y1),N(x2,y2)是反比例函數y=![]() 的圖象上的兩點,且x1<x2,y1<y2,指出點M,N位于哪個象限,并簡要說明理由.
的圖象上的兩點,且x1<x2,y1<y2,指出點M,N位于哪個象限,并簡要說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】當m為何值時,關于x的一元二次方程(2m+1)x2+4mx+2m﹣3=0.
(1)有兩個不相等的實數根;
(2)有兩個相等的實數根;
(3)沒有實數根.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】百貨商店服裝專柜在銷售中發現:某商品的進價為每件40元.當售價為每件60元時,每星期可賣出300件,現需降價處理,且經市場調查:每降價1元,每星期可多賣出20件.為占有市場份額,在確保盈利的前提下.
(1)降價多少元時,每星期盈利為6125元.
(2)降價多少元時,每星期盈利額最大,最大盈利額是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com