
【題目】如圖,矩形ABCD中,AB=4,AD=3,M是邊CD上一點,將△ADM沿直線AM對折,得到△ANM.
(1)當AN平分∠MAB時,求DM的長;
(2)連接BN,當DM=1時,求△ABN的面積;
(3)當射線BN交線段CD于點F時,求DF的最大值.
【答案】(1)DM=![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
試題分析:(1)由折疊性質得∠MAN=∠DAM,證出∠DAM=∠MAN=∠NAB,由三角函數得出DM=ADtan∠DAM=![]() 即可;
即可;
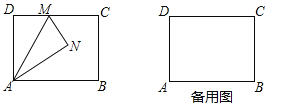
(2)延長MN交AB延長線于點Q,由矩形的性質得出∠DMA=∠MAQ,由折疊性質得出∠DMA=∠AMQ,AN=AD=3,MN=MD=1,得出∠MAQ=∠AMQ,證出MQ=AQ,設NQ=x,則AQ=MQ=1+x,證出∠ANQ=90°,在Rt△ANQ中,由勾股定理得出方程,解方程求出NQ=4,AQ=5,即可求出△ABN的面積;
(3)過點A作AH⊥BF于點H,證明△ABH∽△BFC,得出對應邊成比例![]() ,得出當點N、H重合(即AH=AN)時,AH最大,BH最小,CF最小,DF最大,此時點M、F重合,B、N、M三點共線,由折疊性質得:AD=AH,由AAS證明△ABH≌△BFC,得出CF=BH,由勾股定理求出BH,得出CF,即可得出結果.
,得出當點N、H重合(即AH=AN)時,AH最大,BH最小,CF最小,DF最大,此時點M、F重合,B、N、M三點共線,由折疊性質得:AD=AH,由AAS證明△ABH≌△BFC,得出CF=BH,由勾股定理求出BH,得出CF,即可得出結果.
試題解析:(1)由折疊性質得:△ANM≌△ADM,∴∠MAN=∠DAM,∵AN平分∠MAB,∠MAN=∠NAB,∴∠DAM=∠MAN=∠NAB,∵四邊形ABCD是矩形,∴∠DAB=90°,∴∠DAM=30°,∴DM=ADtan∠DAM=3×tan30°=![]() =
=![]() ;
;
(2)延長MN交AB延長線于點Q,如圖1所示,∵四邊形ABCD是矩形,∴AB∥DC,∴∠DMA=∠MAQ,由折疊性質得:△ANM≌△ADM,∴∠DMA=∠AMQ,AN=AD=3,MN=MD=1,∴∠MAQ=∠AMQ,∴MQ=AQ,設NQ=x,則AQ=MQ=1+x,∵∠ANM=90°,∴∠ANQ=90°,在Rt△ANQ中,由勾股定理得:![]() ,∴
,∴![]() ,解得:x=4,∴NQ=4,AQ=5,∵AB=4,AQ=5,∴S△NAB=
,解得:x=4,∴NQ=4,AQ=5,∵AB=4,AQ=5,∴S△NAB=![]() =
=![]() =
=![]() ANNQ=
ANNQ=![]() ;
;

(3)過點A作AH⊥BF于點H,如圖2所示,∵四邊形ABCD是矩形,∴AB∥DC,∴∠HBA=∠BFC,∵∠AHB=∠BCF=90°,∴△ABH∽△BFC,∴![]() ,∵AH≤AN=3,AB=4,∴當點N、H重合(即AH=AN)時,AH最大,BH最小,CF最小,DF最大,此時點M、F重合,B、N、M三點共線,如圖3所示:
,∵AH≤AN=3,AB=4,∴當點N、H重合(即AH=AN)時,AH最大,BH最小,CF最小,DF最大,此時點M、F重合,B、N、M三點共線,如圖3所示:
由折疊性質得:AD=AH,∵AD=BC,∴AH=BC,在△ABH和△BFC中,∵∠HBA=∠BFC,∠AHB=∠BCF,AH=BC,∴△ABH≌△BFC(AAS),∴CF=BH,由勾股定理得:BH![]() =
=![]() ,∴CF=
,∴CF=![]() ,∴DF的最大值=DC﹣CF=
,∴DF的最大值=DC﹣CF=![]() .
.


科目:初中數學 來源: 題型:
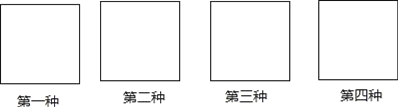
【題目】手工課上,老師要求同學們將邊長為4cm的正方形紙片恰好剪成六個等腰直角三角形,聰明的你請在下列四個正方形中畫出不同的剪裁線,并直接寫出每種不同分割后得到的最小等腰直角三角形面積(注:不同的分法,面積可以相等)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC是等腰直角三角形,AC=BC=2,D是邊AB上一動點(A、B兩點除外),將△CAD繞點C按逆時針方向旋轉角α得到△CEF,其中點E是點A的對應點,點F是點D的對應點.
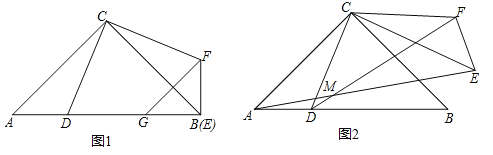
(1)如圖1,當α=90°時,G是邊AB上一點,且BG=AD,連接GF.求證:GF∥AC;
(2)如圖2,當90°≤α≤180°時,AE與DF相交于點M.
①當點M與點C、D不重合時,連接CM,求∠CMD的度數;
②設D為邊AB的中點,當α從90°變化到180°時,求點M運動的路徑長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,有公路l1同側、l2異側的兩個城鎮A,B,電信部門要在S區修建一座信號發射塔,按照設計要求,發射塔到兩個城鎮A,B的距離必須相等,到兩條公路l1,l2的距離也必須相等,發射塔C應修建在什么位置?請用尺規作圖找出所有符合條件的點,注明點C的位置.(保留作圖痕跡,不寫作法)
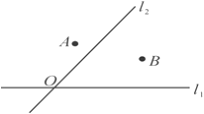
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】設置一種記分的方法:85分以上如88分記為+3分,某個學生在記分表上記為–6分,則這個學生的分數應該是
A. 91分 B. –91分
C. 79分 D. –79分
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在某校“我的中國夢”演講比賽中,有9名學生參加決賽,他們決賽的最終成績各不相同.其中的一名學生想要知道自己能否進入前5名,不僅要了解自己的成績,還要了解這9名學生成績的( ).
A.眾數
B.方差
C.平均數
D.中位數
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,函數y=2x和y=﹣x的圖象分別為直線l1,l2,過點(1,0)作x軸的垂線交l2于點A1,過點A1作y軸的垂線交l2于點A2,過點A2作x軸的垂線交l2于點A3,過點A3作y軸的垂線交l2于點A4,…依次進行下去,則點A2017的坐標為 .
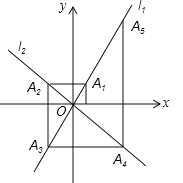
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com