
【題目】如圖,矩形ABCD中,AB=2,BC=5,E、P分別在AD.BC上,且DE=BP=1.連接BE,EC,AP,DP,PD與CE交于點F,AP與BE交于點H.
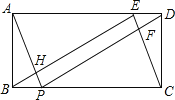
(1)判斷△BEC的形狀,并說明理由;
(2)判斷四邊形EFPH是什么特殊四邊形,并證明你的判斷;
(3)求四邊形EFPH的面積.
【答案】(1)△BEC為直角三角形,理由見解析;(2)四邊形EFPH是矩形,理由見解析;(3)![]()
【解析】
(1)根據矩形的性質可得∠BAE=∠CDE=90°,AB=CD=2,AD=BC=5,然后利用勾股定理即可求出BE和CE,然后根據勾股定理的逆定理即可證出△BEC為直角三角形;
(2)根據矩形的性質可得AD∥BC, AD=BC=5,然后根據平行四邊形的判定定理可得四邊形EBPD和四邊形APCE均為平行四邊形,從而證出四邊形EFPH是平行四邊形,然后根據矩形的定義即可得出結論;
(3)先利用三角形面積的兩種求法,即可求出BH,從而求出HE,然后根據勾股定理即可求出HP,然后根據矩形的面積公式計算即可.
解:(1)△BEC為直角三角形,理由如下
∵四邊形ABCD為矩形
∴∠BAE=∠CDE=90°,AB=CD=2,AD=BC=5
∵DE=1
∴AE=AD-DE=4
在Rt△ABE中,BE=![]()
在Rt△CDE中CE=![]()
∴BE2+CE2=25= BC2
∴△BEC為直角三角形
(2)四邊形EFPH是矩形,理由如下
∵四邊形ABCD為矩形
∴AD∥BC, AD=BC=5
∵DE=BP=1,
∴AD-DE=BC-BP=4
即AE=CP=4
∴四邊形EBPD和四邊形APCE均為平行四邊形
∴EB∥DP,AP∥EC
∴四邊形EFPH是平行四邊形
∵△BEC為直角三角形,∠BEC=90°
∴四邊形EFPH是矩形
(3)∵四邊形APCE為平行四邊形,四邊形EFPH是矩形
∴AP=CE=![]() ,∠EHP=90°
,∠EHP=90°
∴∠BHP=180°-∠EHP=90°
∵S△ABP=![]()
∴![]()
解得:![]()
∴HE=BE-BH=![]()
在Rt△BHP中,HP =![]()
∴S矩形EFPH= HP·HE=![]()


科目:初中數學 來源: 題型:
【題目】近期江蘇省各地均發布“霧霾”黃色預警,我市某口罩廠商生產一種新型口罩產品,每件制造成本為18元,試銷過程中發現,每月銷售量y(萬件)與銷售單價x(元)之間的關系滿足下表.
銷售單價x(元/件) | … | 20 | 25 | 30 | 40 | … |
每月銷售量y(萬件) | … | 60 | 50 | 40 | 20 | … |
(1)請你從所學過的一次函數、二次函數和反比例函數三個模型中確定哪種函數能比較恰當地表示y與x的變化規律,并直接寫出y與x之間的函數關系式為__________;
(2)當銷售單價為多少元時,廠商每月獲得的利潤為440萬元?
(3)如果廠商每月的制造成本不超過540萬元,那么當銷售單價為多少元時,廠商每月獲得的利潤最大?最大利潤為多少萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在同一條道路上,甲車從![]() 地到
地到![]() 地,乙車從
地,乙車從![]() 地到
地到![]() 地,乙先出發,圖中的折線段表示甲、乙兩車之間的距離
地,乙先出發,圖中的折線段表示甲、乙兩車之間的距離![]() (千米)與行駛時間
(千米)與行駛時間![]() (小時)的函數關系的圖象,根據圖象解決以下問題:
(小時)的函數關系的圖象,根據圖象解決以下問題:
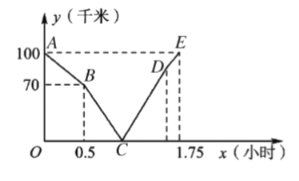
(1)乙先出發的時間為 小時,乙車的速度為 千米/時;
(2)求線段![]() 的函數關系式,并寫出自變量
的函數關系式,并寫出自變量![]() 的取值范圍;
的取值范圍;
(3)甲、乙兩車誰先到終點,先到多少時間?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一張矩形紙片ABCD,其中AD=8cm,AB=6cm,先沿對角線BD對折,點C落在點C′的位置,BC′交AD于點G.
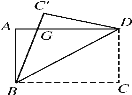
(1)求證:AG=C′G;
(2) 求△BDG的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一次函數y=﹣x+1與拋物線y=![]() x2+bx+c交于A(0,1),B兩點,B點縱坐標為10,拋物線的頂點為C.
x2+bx+c交于A(0,1),B兩點,B點縱坐標為10,拋物線的頂點為C.
(1)求b,c的值;
(2)判斷△ABC的形狀并說明理由;
(3)點D、E分別為線段AB、BC上任意一點,連接CD,取CD的中點F,連接AF,EF.當四邊形ADEF為平行四邊形時,求平行四邊形ADEF的周長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】知識背景
我們在第十一章《三角形》中學習了三角形的邊與角的性質,在第十二章《全等三角形》中學習了全等三角形的性質和判定,在十三章《軸對稱》中學習了等腰三角形的性質和判定.在一些探究題中經常用以上知識轉化角和邊,進而解決問題

問題初探
如圖(1),△ABC中,∠BAC=90°,AB=AC,點D是BC上一點,連接AD,以AD為一邊作△ADE,使∠DAE=90°,AD=AE,連接BE,猜想BE和CD有怎樣的數量關系,并說明理由.
類比再探
如圖(2),△ABC中,∠BAC=90°,AB=AC,點M是AB上一點,點D是BC上一點,連接MD,以MD為一邊作△MDE,使∠DME=90°,MD=ME,連接BE,則∠EBD= .(直接寫出答案,不寫過程,但要求作出輔助線)
方法遷移
如圖(3),△ABC是等邊三角形,點D是BC上一點,連接AD,以AD為一邊作等邊三角形ADE,連接BE,則BD、BE、BC之間有怎樣的數量關系? (直接寫出答案,不寫過程).
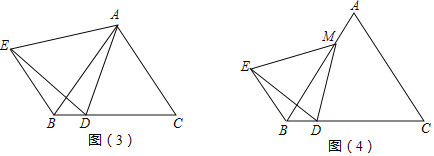
拓展創新
如圖(4),△ABC是等邊三角形,點M是AB上一點,點D是BC上一點,連接MD,以MD為一邊作等邊三角形MDE,連接BE.猜想∠EBD的度數,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
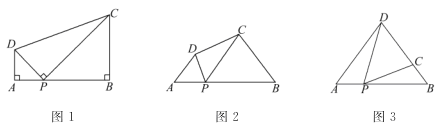
【題目】(1)、問題:如圖1,在四邊形ABCD中,點P為AB上一點,∠DPC=∠A=∠B=90°.求證:AD·BC=AP·BP.
(2)、探究:如圖2,在四邊形ABCD中,點P為AB上一點,當∠DPC=∠A=∠B=θ時,上述結論是否依然成立?說明理由.
(3)、應用:請利用(1)(2)獲得的經驗解決問題:
如圖3,在△ABD中,AB=6,AD=BD=5.點P以每秒1個單位長度的速度,由點A 出發,沿邊AB向點B運動,且滿足∠DPC=∠A.設點P的運動時間為t(秒),當DC的長與△ABD底邊上的高相等時,求t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
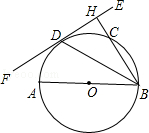
【題目】如圖,AB為⊙O的直徑,EF切⊙O于點D,過點B作BH⊥EF于點H,交⊙O于點C,連接BD.
(1)求證:BD平分∠ABH;
(2)如果AB=12,BC=8,求圓心O到BC的距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com