【題目】一張矩形紙片ABCD，AD=5cm，AB=3cm，將紙片沿ED折疊，A點剛好落在BC邊上的A'處，如圖，這時AE的長應該是（ ） 
A.
cm
B.
cm
C.
cm
D.
cm
【答案】A
【解析】解：∵四邊形ABCD是矩形， ∴AB=CD=3cm，AD=BC=5cm，
∵將紙片沿ED折疊，A點剛好落在BC邊上的A'處，
∴A′D=AD=5cm，A′E=AE，
在Rt△A′CD中，根據勾股定理得，A′C= 
= 
=4cm，
所以，A′B=BC﹣A′C=5﹣4=1cm，
設AE=x，則BE=AB﹣AE=3﹣x，
在Rt△A′EB中，根據勾股定理得，A′B2+BE2=A′E2 ，
即12+（3﹣x）2=x2 ，
解得x= 
，
即AE= cm．
故選A．
【考點精析】本題主要考查了翻折變換（折疊問題）的相關知識點，需要掌握折疊是一種對稱變換，它屬于軸對稱，對稱軸是對應點的連線的垂直平分線，折疊前后圖形的形狀和大小不變，位置變化，對應邊和角相等才能正確解答此題．
科目：初中數學 來源： 題型：
【題目】已知拋物線 
（1）此拋物線的頂點坐標是 ，與x軸的交點坐標是 ， ，與y軸交點坐標是 ，對稱軸直線是 ；
（2）在平面直角坐標系中畫出 的圖象；
（3）結合圖象，說明當x取何值時，y隨x的增大而減小．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點O為平面直角坐標系的原點，點A在x軸上，△OAB是邊長為2的等邊三角形，以O為旋轉中心，將△OAB按順時針方向旋轉60°，得到△OA′B′，那么點A′的坐標為（ ）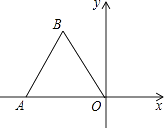
A.（1， 
）
B.（﹣1，2）
C.（﹣1， 
）
D.（﹣1， ）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，拋物線y=ax2+bx﹣3經過A（﹣1，0）B（4，0）兩點，與y軸交于點C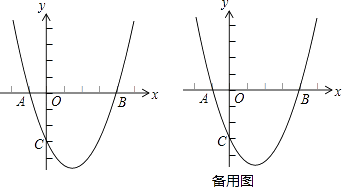
（1）求拋物線解析式；
（2）點N是x軸下方拋物線上的一點，連接AN，若tan∠BAN=2，求點N的縱坐標；
（3）點D是點C關于拋物線對稱軸的對稱點，連接AD，在x軸上是否存在E，使∠AED=∠CAD？如果存在，請直接寫出點E坐標，如果不存在，請說明理由；
（4）連接AC、BC，△ABC的中線BM交y軸于點H，過點A作AG⊥BC，垂足為G，點F是線段BH上的一個動點（不與B、H重合），點F沿線段BH從點B向H移動，移動后的點記作點F′，連接F′C、F′A，△F′AC的F′C、F′A兩邊上的高交于點P，連接AP，CP，△F′AC與△PAC的面積分別記為S1 ， S2 ， S1和S2的乘積記為m，在點F的移動過程中，探究m的值變化情況，若變化，請直接寫出m的變化范圍，若不變，直接寫出這個m值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知，如圖（1），PAB為⊙O的割線，直線PC與⊙O有公共點C，且PC2=PA×PB，
（1）求證：∠PCA=∠PBC；直線PC是⊙O的切線；
（2）如圖（2），作弦CD，使CD⊥AB，連接AD、BC，若AD=2，BC=6，求⊙O的半徑；
（3）如圖（3），若⊙O的半徑為 
，PO= 
，MO=2，∠POM=90°，⊙O上是否存在一點Q，使得PQ+ 
QM有最小值？若存在，請求出這個最小值；若不存在，說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中有一菱形OABC且∠A=120°，點O、B在y軸上，OA=1，現在把菱形向右無滑動翻轉，每次翻轉60°，點B的落點依次為B1、B2、B3…，連續翻轉2017次，則B2017的坐標為 ．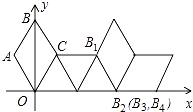 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在△ABC中，AB=AC，∠BAC=2∠DAE=2α．
（1）如圖1，若點D關于直線AE的對稱點為F，求證：△ADF∽△ABC；
（2）如圖2，
在（1）的條件下，若α=45°，求證：DE2=BD2+CE2；
（3）如圖3，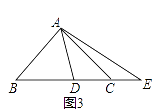
若α=45°，點E在BC的延長線上，則等式DE2=BD2+CE2還能成立嗎？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，是根據某市2010年至2014年工業生產總值繪制的折線統計圖，觀察統計圖獲得以下信息，其中信息判斷錯誤的是（ ） 
A.2010年至2014年間工業生產總值逐年增加
B.2014年的工業生產總值比前一年增加了40億元
C.2012年與2013年每一年與前一年比，其增長額相同
D.從2011年至2014年，每一年與前一年比，2014年的增長率最大
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
