
【題目】問題情境:如圖1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度數. 小明的解題思路是:如圖2,過P作PE∥AB,通過平行線性質,可得∠APC=50°+60°=110°.
問題遷移:
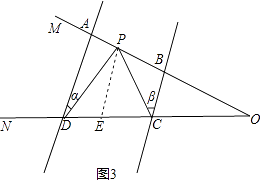
(1)如圖3,AD∥BC,點P在射線OM上運動,當點P在A、B兩點之間運動時,∠ADP=∠α,∠BCP=∠β.試判斷∠CPD、∠α、∠β之間有何數量關系? 請說明理由;
(2)在(1)的條件下,如果點P在A、B兩點外側運動時(點P與點A、B、O三點不重合),請你直接寫出∠CPD、∠α、∠β間的數量關系.
【答案】
(1)解:∠CPD=∠α+∠β,理由如下:
如圖3,過P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE+∠CPE=∠α+∠β;
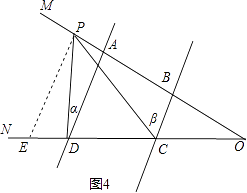
(2)解:當P在BA延長線時,∠CPD=∠β﹣∠α;
理由:如圖4,過P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠CPE﹣∠DPE=∠β﹣∠α;
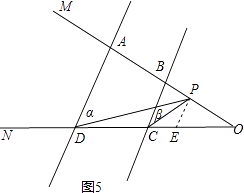
當P在AB延長線時,∠CPD=∠α﹣∠β.
理由:如圖5,過P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE﹣∠CPE=∠α﹣∠β.
【解析】(1)過P作PE∥AD交CD于E,推出AD∥PE∥BC,根據平行線的性質得出∠α=∠DPE,∠β=∠CPE,即可得出答案;(2)畫出圖形(分兩種情況:①點P在BA的延長線上,②點P在AB的延長線上),根據平行線的性質得出∠α=∠DPE,∠β=∠CPE,即可得出答案.
【考點精析】掌握平行線的性質是解答本題的根本,需要知道兩直線平行,同位角相等;兩直線平行,內錯角相等;兩直線平行,同旁內角互補.


科目:初中數學 來源: 題型:
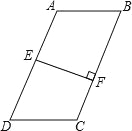
【題目】如圖,在四邊形ABCD中,AB∥DC,E是AD中點,EF⊥BC于點F,BC=5,EF=3.
(1)若AB=DC,則四邊形ABCD的面積S= ;
(2)若AB>DC,則此時四邊形ABCD的面積S′ S(用“>”或“=”或“<”填空).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將1、 ![]() 、
、 ![]() 、
、 ![]() 按如圖方式排列,若規定(m,n)表示第m排從左向右第n個數,則(6,5)與(13,6)表示的兩數之積是( )
按如圖方式排列,若規定(m,n)表示第m排從左向右第n個數,則(6,5)與(13,6)表示的兩數之積是( ) 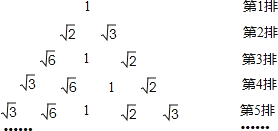
A.![]()
B.6
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某農機廠四月份生產零件40萬個,第二季度共生產零件162萬個.設該廠五、六月份平均每月的增長率為x,那么x滿足的方程是( )
A.40(1+x)2=162
B.40+40(1+x)+40(1+x)2=162
C.40(1+2x)=162
D.40+40(1+x)+40(1+2x)=162
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com