
【題目】如圖,在四邊形ABCD中,AD∥BC,DE⊥BC,垂足為點(diǎn)E,連接AC交DE于點(diǎn)F,點(diǎn)G為AF的中點(diǎn),∠ACD=2∠ACB.若DG=3,EC=1,則DE的長為( ) 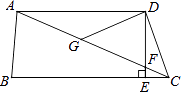
A.2 ![]()
B.![]()
C.2 ![]()
D.![]()
【答案】C
【解析】解:∵AD∥BC,DE⊥BC, ∴DE⊥AD,∠CAD=∠ACB,∠ADE=∠BED=90°,
又∵點(diǎn)G為AF的中點(diǎn),
∴DG=AG,
∴∠GAD=∠GDA,
∴∠CGD=2∠CAD,
∵∠ACD=2∠ACB=2∠CAD,
∴∠ACD=∠CGD,
∴CD=DG=3,
在Rt△CED中,DE= ![]() =2
=2 ![]() .
.
故選:C.
根據(jù)直角三角形斜邊上的中線的性質(zhì)可得DG=AG,根據(jù)等腰三角形的性質(zhì)可得∠GAD=∠GDA,根據(jù)三角形外角的性質(zhì)可得∠CGD=2∠GAD,再根據(jù)平行線的性質(zhì)和等量關(guān)系可得∠ACD=∠CGD,根據(jù)等腰三角形的性質(zhì)可得CD=DG,再根據(jù)勾股定理即可求解.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】下列事件是必然事件的是( )
A. 明年國慶節(jié)寧波的天氣是晴天B. 小華上學(xué)的路上遇到同班同學(xué)
C. 任意擲一枚均勻的硬幣,正面朝上D. 在學(xué)校操場上拋出的籃球會(huì)下落
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】計(jì)算:
(1)﹣22×7﹣(﹣3)×6+5;
(2)( ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() )×24÷(﹣2);
)×24÷(﹣2);
(3)56×1 ![]() +56×(﹣
+56×(﹣ ![]() )﹣56×
)﹣56× ![]() ;
;
(4)(﹣1)4﹣ ![]() ×[2﹣(﹣3)2].
×[2﹣(﹣3)2].
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩人在同一直線噵路上同起點(diǎn),同方向同進(jìn)出發(fā),分別以不同的速度勻速跑步1500米,當(dāng)甲超出乙200米時(shí),甲停下來等候乙,甲、乙會(huì)合后,兩人分別以原來的速度繼續(xù)跑向終點(diǎn),先到達(dá)終點(diǎn)的人在終點(diǎn)休息,在跑步的整個(gè)過程中,甲、乙兩人的距離y(米)與出發(fā)的時(shí)間x(秒)之間的關(guān)系如圖所示,則甲到終點(diǎn)時(shí),乙距離終點(diǎn)______________米。
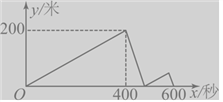
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】所謂氣質(zhì),是指嬰兒出生后最早表示出來的以一種較為明顯而穩(wěn)定的人格特征類型,也指孩子對(duì)身體內(nèi)在或外來刺激反應(yīng)的方式。心理學(xué)界常將氣質(zhì)分為四大類:膽汁型、多血質(zhì)、黏液質(zhì)、抑郁質(zhì)。我校心理協(xié)會(huì)為了更好的了解學(xué)生,在高中隨機(jī)發(fā)放了若干份問卷調(diào)查,并將統(tǒng)計(jì)結(jié)果繪制成如下圖表:
四種氣質(zhì)類型人數(shù)頻數(shù)分布表 | 黏液質(zhì)氣質(zhì)各年級(jí)人數(shù)頻數(shù)分布直方圖 | |||||||||||||||
|
|
根據(jù)以上信息完成下列問題并補(bǔ)全頻數(shù)分布直方圖:
(1)![]() _______,
_______, ![]() _______
_______
(2)請(qǐng)你估計(jì)一下,高三年級(jí)1200名學(xué)生中,膽汁型和多血質(zhì)的共有多少人?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,反比例函數(shù)![]() (n為常數(shù),
(n為常數(shù), ![]() )的圖象與一次函數(shù)
)的圖象與一次函數(shù)![]() (k、b為常數(shù),
(k、b為常數(shù), ![]() )的圖象在第一象限內(nèi)交于點(diǎn)C
)的圖象在第一象限內(nèi)交于點(diǎn)C![]() ,一次函數(shù)
,一次函數(shù)![]() 與x軸、y軸分別交于A、B兩點(diǎn)。已知
與x軸、y軸分別交于A、B兩點(diǎn)。已知![]() ,
, ![]() 。
。
(1)求一次函數(shù)的解析式和反比例函數(shù)的解析式;
(2)若點(diǎn)P在x軸上且使得![]() 面積為
面積為![]() 面積的3倍,求滿足條件的P點(diǎn)坐標(biāo)。
面積的3倍,求滿足條件的P點(diǎn)坐標(biāo)。
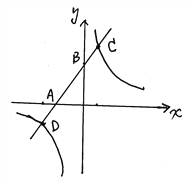
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(1)如圖①已知∠ACB=∠DCE=90°,AC=BC=4,CE=CD,AE=2,∠CAE=45°,求AD的長.
(2)如圖②已知∠ACB=∠DCE=90°,∠ABC=∠DEC=∠CAE=30°,AC=2,AE=4![]() ,求AD的長.
,求AD的長.
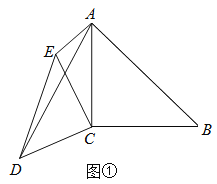

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知蝸牛從A點(diǎn)出發(fā),在一條數(shù)軸上來回爬行,規(guī)定:向正半軸運(yùn)動(dòng)記作“+”,向負(fù)半軸運(yùn)動(dòng)記作“﹣”,從開始到結(jié)束爬行的各段路程(單位:cm)依次為:+7,﹣5,﹣10,﹣8,+9,﹣6,+12,+4
(1)若A點(diǎn)在數(shù)軸上表示的數(shù)為﹣3,則蝸牛停在數(shù)軸上何處,請(qǐng)通過計(jì)算加以說明;
(2)若蝸牛的爬行速度為每秒 ![]() cm,請(qǐng)問蝸牛一共爬行了多少秒?
cm,請(qǐng)問蝸牛一共爬行了多少秒?
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com