
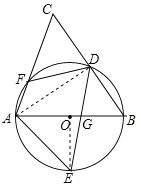
【題目】如圖,AB是⊙O的直徑,D、E為⊙O上位于AB異側的兩點,連接BD并延長至點C,使得CD=BD,連接AC交⊙O于點F,連接AE、DE、DF.
(1)證明:∠E=∠C;
(2)若∠E=55°,求∠BDF的度數;
(3)設DE交AB于點G,若DF=4,cosB=![]() ,E是弧AB的中點,求EGED的值.
,E是弧AB的中點,求EGED的值.

【答案】(1)見解析;(2)∠BDF=110°;(3)18
【解析】試題解析:(1)直接利用圓周角定理得出AD⊥BC,勁兒利用線段垂直平分線的性質得出AB=AC,即可得出∠E=∠C;
(2)利用圓內接四邊形的性質得出∠AFD=180°﹣∠E,進而得出∠BDF=∠C+∠CFD,即可得出答案;
(3)根據cosB=![]() ,得出AB的長,再求出AE的長,進而得出△AEG∽△DEA,求出答案即可.
,得出AB的長,再求出AE的長,進而得出△AEG∽△DEA,求出答案即可.
試題解析:(1)證明:連接AD,∵AB是⊙O的直徑,∴∠ADB=90°,即AD⊥BC,∵CD=BD,∴AD垂直平分BC,∴AB=AC,∴∠B=∠C,又∵∠B=∠E,∴∠E=∠C;
(2)解:∵四邊形AEDF是⊙O的內接四邊形,∴∠AFD=180°﹣∠E,又∵∠CFD=180°﹣∠AFD,∴∠CFD=∠E=55°,又∵∠E=∠C=55°,∴∠BDF=∠C+∠CFD=110°;
(3)解:連接OE,∵∠CFD=∠E=∠C,∴FD=CD=BD=4,在Rt△ABD中,cosB=![]() ,BD=4,∴AB=6,∵E是
,BD=4,∴AB=6,∵E是![]() 的中點,AB是⊙O的直徑,∴∠AOE=90°,∵AO=OE=3,∴AE=
的中點,AB是⊙O的直徑,∴∠AOE=90°,∵AO=OE=3,∴AE=![]() ,∵E是
,∵E是![]() 的中點,∴∠ADE=∠EAB,∴△AEG∽△DEA,∴
的中點,∴∠ADE=∠EAB,∴△AEG∽△DEA,∴![]() ,即EGED=
,即EGED=![]() =18.
=18.


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:初中數學 來源: 題型:
【題目】綜合與實踐
問題情境
數學活動課上,老師讓同學們以“三角形平移與旋轉”為主題開展數學活動,![]() 和
和![]() 是兩個等邊三角形紙片,其中,
是兩個等邊三角形紙片,其中,![]() .
.
解決問題
(1)勤奮小組將![]() 和
和![]() 按圖1所示的方式擺放(點
按圖1所示的方式擺放(點![]() 在同一條直線上) ,連接
在同一條直線上) ,連接![]() .發現
.發現![]() ,請你給予證明;
,請你給予證明;

(2)如圖2,創新小組在勤奮小組的基礎上繼續探究,將![]() 繞著點
繞著點![]() 逆時針方向旋轉,當點
逆時針方向旋轉,當點![]() 恰好落在
恰好落在![]() 邊上時,求
邊上時,求![]() 的面積;
的面積;

拓展延伸
(3)如圖3,縝密小組在創新小組的基礎上,提出一個問題: “將![]() 沿
沿![]() 方向平移
方向平移![]() 得到
得到![]() 連接
連接![]() ,當
,當![]() 恰好是以
恰好是以![]() 為斜邊的直角三角形時,求
為斜邊的直角三角形時,求![]() 的值.請你直接寫出
的值.請你直接寫出![]() 的值.
的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某賓館有50個房間供游客住宿,當每個房間的房價為每天180元時,房間會全部住滿.當每個房間 每天的房價每增加10元時,就會有一個房間空閑.賓館需對游客居住的每個房間每天支出20元的各種費用.根據規定,每個房間每天的房價不得高于340元.設每個房間的房價增加x元(x為10的正整數倍).
(1)設一天訂住的房間數為y,直接寫出y與x的函數關系式及自變量x的取值范圍;
(2)設賓館一天的利潤為w元,求w與x的函數關系式;
(3)一天訂住多少個房間時,賓館的利潤最大?最大利潤是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場推出兩種優惠方法,甲種方法:購買一個書包贈送一支筆;乙種方法:購買書包和筆一律按九折優惠,書包20元/個,筆5元/支,小明和同學需購買4個書包,筆若干(不少于4支).
(1)分別寫出兩種方式購買的費用y(元)與所買筆支數x(支)之間的函數關系式;
(2)如果商場允許可以任意選擇一種優惠方式,也可以同時用兩種方式購買,請你就購買4個書包12支筆,設計一種最省錢的購買方式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,A城氣象臺測得臺風中心在A城正西方向600km的B處,以每小時200km的速度向北偏東60°的方向移動,距臺風中心500km的范圍內是受臺風影響的區域.
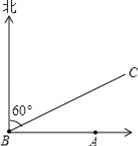
(1)A城是否受到這次臺風的影響?為什么?
(2)若A城受到這次臺風的影響,那么A城遭受這次臺風影響有多長時間?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用四塊完全相同的小長方形拼成的一個“回形”正方形.

(1)用不同代數式表示圖中的陰影部分的面積,你能得到怎樣的等式:________;
(2)利用(1)中的結論.計算:![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)根據(1)的結論.若![]() .求
.求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面材料:
一個含有多個字母的式子中,如果任意交換兩個字母的位置,式子的值都不變,這樣的式子就叫做對稱式,例如:![]() ,
,![]() ,
,![]() ,…含有兩個字母
,…含有兩個字母![]() ,
,![]() 的對稱式的基本對稱式是
的對稱式的基本對稱式是![]() 和
和![]() ,像
,像![]() ,
,![]() 等對稱式都可以用
等對稱式都可以用![]() ,
,![]() 表示,例如:
表示,例如:![]() .
.
請根據以上材料解決下列問題:
(1)式子:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 中,屬于對稱式的是 (填序號)
中,屬于對稱式的是 (填序號)
(2)已知![]() .
.
①若![]() ,求對稱式
,求對稱式![]() 的值
的值
②若![]() ,求對稱式
,求對稱式![]() 的最大值
的最大值
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠B>∠C,AD是BC邊上的高,AE平分∠BAC.
(1)若∠B=50°,∠C=30°,則∠DAE= .
(2)若∠B=60°,∠C=20°,則∠DAE= .
(3)由(1)(2)猜想∠DAE與∠B,∠C之間的關系為 ,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩商場以同樣價格出售同樣的商品,并且各自又推出不同的優惠方案:
甲商場:購物超過200元后,超出200元的部分按90%收費;
乙商場:購物超過100元后,超出100元的部分按95%收費.
設小李在同一商場購買商品的原價總和為![]() 元,則甲商場消費的金額為
元,則甲商場消費的金額為![]() 元,乙商場消費的金額為
元,乙商場消費的金額為![]() 元.
元.
(1)請分別求出![]() ,
,![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(2)當![]() 元時,小李在哪家商場購物更合算?
元時,小李在哪家商場購物更合算?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com