Question

【題目】如圖，已知在△ABC中，∠BAC的平分線與線段BC的垂直平分線PQ相交于點P，過點P分別作PN垂直于AB于點N，PM垂直于AC于點M，BN和CM有什么數量關系？請說明理由．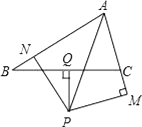

Answer 1

【答案】解：BN=CM，理由如下：
如圖，連接PB，PC，
∵AP是∠BAC的平分線，PN⊥AB，PM⊥AC，
∴PM=PN，∠PMC=∠PNB=90°，
∵P在BC的垂直平分線上，
∴PC=PB，
在Rt△PMC和Rt△PNB中， ，
∴Rt△PMC≌Rt△PNB（HL），
∴BN=CM．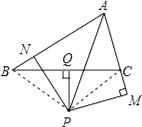

【解析】連接PB，PC，根據角平分線性質求出PM=PN，根據線段垂直平分線求出PB=PC，根據HL證Rt△PMC≌Rt△PNB，即可得出答案．
【考點精析】認真審題，首先需要了解角平分線的性質定理(定理1：在角的平分線上的點到這個角的兩邊的距離相等； 定理2：一個角的兩邊的距離相等的點，在這個角的平分線上)，還要掌握線段垂直平分線的性質(垂直于一條線段并且平分這條線段的直線是這條線段的垂直平分線；線段垂直平分線的性質定理：線段垂直平分線上的點和這條線段兩個端點的距離相等)的相關知識才是答題的關鍵．