
【題目】如圖,△EAF=15°,AB=BC=CD=DE=EF,則∠DEF等于( ) 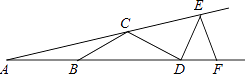
A.90°
B.75°
C.70°
D.60°
【答案】D
【解析】解:∵AB=BC=CD=DE=EF,∠A=15°, ∴∠BCA=∠A=15°,
∴∠CBD=∠BDC=∠BCA+∠A=15°+15°=30°,
∴∠BCD=180°﹣(∠CBD+∠BDC)=180°﹣60°=120°,
∴∠ECD=∠CED=180°﹣∠BCD﹣∠BCA=180°﹣120°﹣15°=45°,
∴∠CDE=180°﹣(∠ECD+∠CED)=180°﹣90°=90°,
∴∠EDF=∠EFD=180°﹣∠CDE﹣∠BDC=180°﹣90°﹣30°=60°,
∴∠DEF=180°﹣(∠EDF+∠EFC)=180°﹣120°=60°.
故選D.
【考點精析】根據題目的已知條件,利用等腰三角形的性質的相關知識可以得到問題的答案,需要掌握等腰三角形的兩個底角相等(簡稱:等邊對等角).


科目:初中數學 來源: 題型:
【題目】在下列說法中是錯誤的是( )
A.在△ABC中,若∠A:∠B:∠C=5:2:3,則△ABC為直角三角形
B.在△ABC中,∠C=∠A﹣∠B,則△ABC為直角三角形
C.在△ABC中,若a= ![]() c,b=
c,b= ![]() c,則△ABC為直角三角形
c,則△ABC為直角三角形
D.在△ABC中,若a:b:c=2:2:4,則△ABC為直角三角形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】浙江省統計局發布的數據顯示,2018年末,全省常住人口為5737萬人.數據“5737萬”用科學記數法表示為( )
A.5737×l04B.57.37×106C.5.737×107D.5.737×108
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將第一個圖(圖①)所示的正三角形連結各邊中點進行分割,得到第二個圖(圖②);再將第二個圖中最中間的小正三角形按同樣的方式進行分割,得到第三個圖(圖③);再將第三個圖中最中間的小正三角形按同樣的方式進行分割,…,則得到的第五個圖中,共有個正三角形.( ) 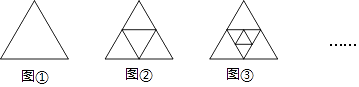
A.14
B.15
C.16
D.17
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖在數軸上A點表示數a,B點表示數b,a、b滿足|a+2|+|b﹣4|=0.![]()
(1)點A表示的數為;點B表示的數為;
(2)一小球甲從點A處以1個單位/秒的速度向左運動;同時另一小球乙從點B處以2個單位/秒的速度也向左運動,設運動的時間為t(秒),
①當t=1時,甲小球到原點的距離為;乙小球到原點的距離為;當t=3時,甲小球到原點的距離為;乙小球到原點的距離為;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果P 是正方形ABCD 內的一點,且滿足∠APB+∠DPC=180°,那么稱點P 是正方形 ABCD 的“對補點”.
(1)如圖1,正方形ABCD 的對角線AC,BD 交于點M,求證:點M 是正方形ABCD 的對補點;
(2)如圖2,在平面直角坐標系中,正方形ABCD 的頂點A(1,1),C(3,3).除對角線交點外,請再寫出一個該正方形的對補點的坐標,并證明.
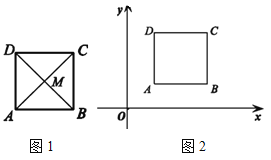
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將矩形紙片ABCD折疊,使點D與點B重合,點C落在C′處,折痕為EF,若AB=1,BC=2,則△ABE和BC′F的周長之和為( ) 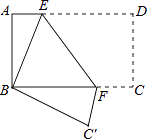
A.3
B.4
C.6
D.8
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com