
【題目】如圖,在⊙O中,半徑OA⊥OB,過OA的中點C作FD∥OB交⊙O于D、F兩點,且CD=![]() ,以O為圓心,OC為半徑作
,以O為圓心,OC為半徑作![]() ,交OB于E點.
,交OB于E點.
(1)求⊙O的半徑OA的長;
(2)計算陰影部分的面積.

科目:初中數學 來源: 題型:
【題目】如圖1,長方形![]() 的邊
的邊![]() 在數軸上,
在數軸上,![]() 為原點,長方形
為原點,長方形![]() 的面積為12,
的面積為12,![]() 邊的長為3
邊的長為3
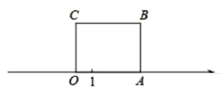
(1)數軸上點![]() 表示的數為
表示的數為
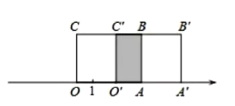
(2)將長方形![]() 沿數軸水平移動,移動后的長方形記為
沿數軸水平移動,移動后的長方形記為![]() ,設長方形
,設長方形![]() 移動的距離為
移動的距離為![]() ,移動后的長方形
,移動后的長方形![]() 與原長方形
與原長方形![]() 重疊部分的面積記為
重疊部分的面積記為![]()
①當![]() 等于原長方形
等于原長方形![]() 面積的
面積的![]() 時,則點
時,則點![]() 的移動距離
的移動距離![]() ,此時數軸上點
,此時數軸上點![]() 表示的數為
表示的數為
②![]() 為線段
為線段![]() 的中點,點
的中點,點![]() 在線段
在線段![]() 上,且
上,且![]() 當點
當點![]() 所表示的數互為相反數時,則
所表示的數互為相反數時,則![]() 的值為
的值為
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,四邊形ABCD是梯形,AB、CD相互平行,在AB上有兩點E和F,此時四邊形DCFE恰好是正方形,已知CD=a,AD=a+ab2,BC=a+2ab2,(單位:米)其中a>0,1<b2<4,現有甲乙兩只媽蟻,甲螞蟻從A點出發,沿著A﹣D﹣C﹣F﹣A的路線行走,乙螞蟻從B點出發,沿著B﹣C﹣D﹣E﹣B的路線行走,甲乙同時出發,各自走回A和B點時停止.甲的速度是![]() (米/秒),乙的速度是
(米/秒),乙的速度是![]() (米/秒).
(米/秒).
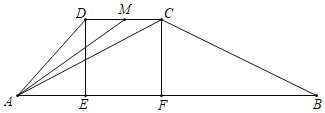
(1)用含a、b的代數式表示:
①甲走到點C時,用時 秒;
②當甲走到點C時,乙走了 米;
③當甲走到點C時,此時乙在點M處,△AMC的面積是 平方米;
④當甲走到點C時,已經和乙相遇一次,它們從出發到這一次相遇,用時 秒.
(2)它們還會有第二次相遇嗎?如果有,請求出兩只螞蟻從出發到第二次相遇所用的時間.如果沒有,簡要說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,∠B=∠C=90°,AB>CD,AD=AB+CD,∠ADC的平分線DE,交BC于點E.
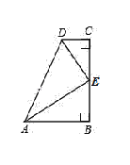
證明:①EC=EB;②AE⊥DE.
查看答案和解析>>
科目:初中數學 來源: 題型:
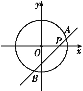
【題目】如圖,在平面直角坐標系中, ⊙O的半徑是1,直線AB與x軸交于點P(x,0),且與x軸的正半軸夾角為45°,若直線AB與⊙O有公共點,則x值的范圍是( )
A. -1≤x≤1 B. -![]() ≤x≤
≤x≤![]() C. -
C. -![]() <x<
<x<![]() D. 0≤x≤
D. 0≤x≤![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下面三行單項式:
![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…;①
,…;①
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…;②
,…;②
![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() ,…;③
,…;③
根據你發現的規律,解答下列問題:
(1)第①行的第8個單項式為 ;
(2)第②行的第9個單項式為 ;
(3)第③行的第n個單項式為 (用含n的式子表示);
(4)取每行的第8個單項式,令這三個單項式的和為A.
當![]() 時,求A的值.
時,求A的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是正方形,E是線段CD上的點,將△ADE沿AE對折得到△AFE,直線EF交邊BC于點G,連接AG.
(1)求證:△ABG≌△AFG;
(2)當DE是CD的一半時,求∠EAG的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,A(﹣2,0),B(0,4),以B點為直角頂點在第二象限作等腰直角△ABC.
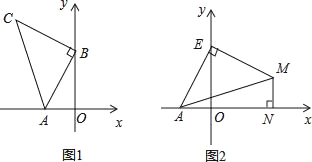
(1)求C點的坐標;
(2)在坐標平面內是否存在一點P,使△PAB與△ABC全等?若存在,求出P點坐標,若不存在,請說明理由;
(3)如圖2,點E為y軸正半軸上一動點,以E為直角頂點作等腰直角△AEM,過M作MN⊥x軸于N,求OE﹣MN的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com