
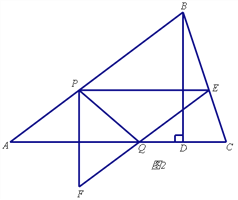
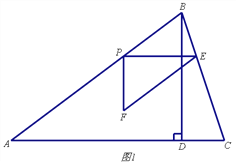
【題目】如圖1,在銳角△ABC中,AB=5,tanC=3,BD⊥AC于點D,BD=3,點P從點A出發(fā),以每秒1個單位長度的速度沿AB向終點B運動,過點P作PE∥AC交邊BC于點E,以PE為邊作Rt△PEF,使∠EPF=90°,點F在點P的下方,且EF∥AB.設△PEF與△ABD重疊部分圖形的面積為S(平方單位)(S>0),點P的運動時間為t(秒)
(t>0).
(1)求線段AC的長.
(2)當△PEF與△ABD重疊部分圖形為四邊形時,求S與t之間的函數(shù)關系式,并寫出t的取值范圍.
(3)若邊EF所在直線與邊AC交于點Q,連結PQ,如圖2,直接寫出△ABC的某一頂點到P、Q兩點距離相等時t的值.
【答案】(1)5(2)S=![]() (5﹣t)2(3)綜上所述,t=
(5﹣t)2(3)綜上所述,t=![]() s或
s或![]() s或
s或![]() s時,滿足題目要求
s時,滿足題目要求
【解析】分析: (1)在Rt△ABD中,利用勾股定理求出AD,在Rt△BDC中,求出CD即可.
(2)分2種情形求解:如圖1中,當0<t≤1時,重疊部分是四邊形PMDN.如圖2中,當![]() ≤t<5時,重疊部分是四邊形PNMF.
≤t<5時,重疊部分是四邊形PNMF.
(3)如圖5中,當PQ的垂直平分線經過當A時.根據(jù)PE=PA,可得t=5-t解決問題.如圖6中,當PQ的垂直平分線經過點B時,作EN⊥AC于N,EP交BD于M.在Rt△BQD中,根據(jù)BQ2=QD2+BD2,列出方程即可解決問題.
詳解:
(1)在Rt△ABD中,∠BDA=90°,AB=5,BD=3,
∴AD=![]() =
=![]() =4,
=4,
在Rt△BCD中,∠BDC=90°,BD=3,tanc=3,∴CD=![]() =
=![]() =1,
=1,
∴AC=AD+CD=4+1=5.
(2)如圖1中,當0<t≤1時,重疊部分是四邊形PMDN.
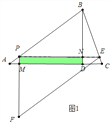


易知PA=t,AM=![]() t,PM=
t,PM=![]() t,DM=4﹣
t,DM=4﹣![]() t,
t,
∴S=![]() t(4﹣
t(4﹣![]() t)=﹣
t)=﹣![]() t2+
t2+![]() t.
t.
如圖2中,當![]() ≤t<5時,重疊部分是四邊形PNMF.
≤t<5時,重疊部分是四邊形PNMF.
∵AB=5,AC=AD+CD=4+1=5,
∴AC=AB,
易證PB=PE=5﹣t,PF=![]() (5﹣t),PN=
(5﹣t),PN=![]() (5﹣t),
(5﹣t),
S=![]() (5﹣t)
(5﹣t)![]() (5﹣t)﹣
(5﹣t)﹣![]()
![]() (5﹣t)
(5﹣t)![]()
![]() (5﹣t)=
(5﹣t)=![]() (5﹣t)2.
(5﹣t)2.
(3)如圖3中,當A到P、Q距離相等時.
易知四邊形APEQ時菱形,∴PE=PA,即t=5﹣t,∴t=![]() .
.
如圖4中,當B到P、Q距離相等時,作EN⊥AC于N,EP交BD于M.


易知四邊形PENG是矩形,四邊形DMEN是矩形,∴PG=EN=![]() t,EM=DN=PE﹣PM=
t,EM=DN=PE﹣PM=![]() (5﹣t),
(5﹣t),
QN=![]() EN=
EN=![]() t,∴QD=4﹣(5﹣t)=t﹣1,在Rt△BQD中,∵BQ2=QD2+BD2,
t,∴QD=4﹣(5﹣t)=t﹣1,在Rt△BQD中,∵BQ2=QD2+BD2,
∴(5﹣t)2=32+(t﹣1)2,∴t=![]() .
.
如圖5中,當C到P、Q距離相等時,作PM⊥AC與M,連接PC.
由PC=CQ,可得:(![]() t)2+(5﹣
t)2+(5﹣![]() t)2=t2,解得t=
t)2=t2,解得t=![]()
綜上所述,t=![]() s或
s或![]() s或
s或![]() s時,滿足題目要求.
s時,滿足題目要求.
點睛: 本題考查三角形綜合題、解直角三角形、勾股定理、銳角三角函數(shù)等知識,解題的關鍵是靈活運用所學知識解決問題,學會用分類討論的思想思考問題,學會構建方程解決問題,屬于中考壓軸題.


 一課一練課時達標系列答案
一課一練課時達標系列答案 期末寶典單元檢測分類復習卷系列答案
期末寶典單元檢測分類復習卷系列答案科目:初中數(shù)學 來源: 題型:
【題目】如圖:已知![]() ,對應的坐標如下,請利用學過的變換(平移、旋轉、軸對稱)知識經過若干次圖形變化,使得點A與點E重合、點B與點D重合,寫出一種變化的過程_____.
,對應的坐標如下,請利用學過的變換(平移、旋轉、軸對稱)知識經過若干次圖形變化,使得點A與點E重合、點B與點D重合,寫出一種變化的過程_____.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】新定義:[a,b,c]為二次函數(shù)y=ax2+bx+e(a≠0,a,b,c為實數(shù))的“圖象數(shù)”,如:y=-x2+2x+3的“圖象數(shù)”為[-1,2,3]
(1)二次函數(shù)y=![]() x2-x-1的“圖象數(shù)”為 .
x2-x-1的“圖象數(shù)”為 .
(2)若圖象數(shù)”是[m,m+1,m+1]的二次函數(shù)的圖象與x軸只有一個交點,求m的值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=90°,AC=8,BC=6.CD⊥AB于點D.點P從點A出發(fā),以每秒1個單位長度的速度沿線段AB向終點B運動.在運動過程中,以點P為頂點作長為2,寬為1的矩形PQMN,其中PQ=2,PN=1,點Q在點P的左側,MN在PQ的下分,且PQ總保持與AC垂直.設P的運動時間為t(秒)(t>0),矩形PQMN與△ACD的重疊部分圖形面積為S(平方單位).
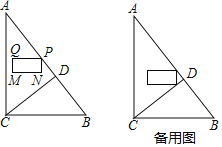
(1)求線段CD的長;
(2)當矩形PQMN與線段CD有公共點時,求t的取值范圍;
(3)當點P在線段AD上運動時,求S與t的函數(shù)關系式.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知拋物線y=ax2﹣8ax+12a(a<0)與x軸交于A、B兩點(點A在點B的左邊),拋物線上另有一點C在第一象限,且使△OCA∽△OBC,
(1)求OC的長及![]() 的值;
的值;
(2)設直線BC與y軸交于P點,當點C恰好在OP的垂直平分線上時,求直線BP和拋物線的解析式.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】問題情境
在綜合與實踐課上,老師讓同學們以“兩條平行線AB,CD和一塊含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”為主題開展數(shù)學活動.
操作發(fā)現(xiàn)
(1)如圖(1),小明把三角尺的60°角的頂點G放在CD上,若∠2=2∠1,求∠1的度數(shù);
(2)如圖(2),小穎把三角尺的兩個銳角的頂點E、G分別放在AB和CD上,請你探索并說明∠AEF與∠FGC之間的數(shù)量關系;
結論應用
(3)如圖(3),小亮把三角尺的直角頂點F放在CD上,30°角的頂點E落在AB上.若∠AEG=α,則∠CFG等于______(用含α的式子表示).

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】有一張長方形紙片![]() (如圖①),
(如圖①),![]() ,將紙片折疊,使
,將紙片折疊,使![]() 落在
落在![]() 邊上,
邊上,![]() 為
為![]() 的對應點,折痕為
的對應點,折痕為![]() (如圖②),再將長方形
(如圖②),再將長方形![]() 以
以![]() 為折痕向右折疊,若點
為折痕向右折疊,若點![]() 落在
落在![]() 的三等分點上,則
的三等分點上,則![]() 的長為( )
的長為( )

A.8B.10C.8或10D.8或12
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】材料:思考的同學小斌在解決連比等式問題:“已知正數(shù)![]() ,
,![]() ,
,![]() 滿足
滿足![]() ,求
,求![]() 的值”時,采用了引入?yún)?shù)法
的值”時,采用了引入?yún)?shù)法![]() ,將連比等式轉化為了三個等式,再利用等式的基本性質求出參數(shù)的值.進而得出
,將連比等式轉化為了三個等式,再利用等式的基本性質求出參數(shù)的值.進而得出![]() ,
,![]() ,
,![]() 之間的關系,從而解決問題.過程如下:
之間的關系,從而解決問題.過程如下:
解;設![]() ,則有:
,則有:
![]() ,
,![]() ,
,![]() ,
,
將以上三個等式相加,得![]() .
.
![]()
![]() ,
,![]() ,
,![]() 都為正數(shù),
都為正數(shù),
![]()
![]() ,即
,即![]() ,.
,.
![]()
![]() .
.
仔細閱讀上述材料,解決下面的問題:
(1)若正數(shù)![]() ,
,![]() ,
,![]() 滿足
滿足![]() ,求
,求![]() 的值;
的值;
(2)已知![]() ,
,![]() ,
,![]() ,
,![]() 互不相等,求證:
互不相等,求證:![]() .
.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
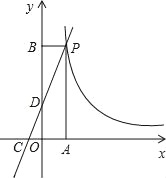
【題目】如圖,一次函數(shù)y=kx+2的圖象與反比例函數(shù)y=![]() 的圖象在第一象限的交點為P,PA⊥x軸于點A,PB⊥y軸于點B,函數(shù)y=kx+2的圖象分別交x軸,y軸于點C,D,已知△OCD的面積S△OCD=1,
的圖象在第一象限的交點為P,PA⊥x軸于點A,PB⊥y軸于點B,函數(shù)y=kx+2的圖象分別交x軸,y軸于點C,D,已知△OCD的面積S△OCD=1,![]() =
=![]()
(1)求點D的坐標;
(2)求k,m的值;
(3)寫出當x>0時,使一次函數(shù)y=kx+2的值大于反比例函數(shù)y=![]() 的值x的取值范圍.
的值x的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com