
【題目】如圖,直線y=﹣ ![]() x+c與x軸交于點A(3,0),與y軸交于點B,拋物線y=﹣
x+c與x軸交于點A(3,0),與y軸交于點B,拋物線y=﹣ ![]() x2+bx+c經過點A,B.
x2+bx+c經過點A,B.
(1)求點B的坐標和拋物線的解析式;
(2)M(m,0)為x軸上一動點,過點M且垂直于x軸的直線與直線AB及拋物線分別交于點P,N.
①點M在線段OA上運動,若以B,P,N為頂點的三角形與△APM相似,求點M的坐標;
②點M在x軸上自由運動,若三個點M,P,N中恰有一點是其它兩點所連線段的中點(三點重合除外),則稱M,P,N三點為“共諧點”.請直接寫出使得M,P,N三點成為“共諧點”的m的值.
【答案】
(1)
解:∵y=﹣ ![]() x+c與x軸交于點A(3,0),與y軸交于點B,
x+c與x軸交于點A(3,0),與y軸交于點B,
∴0=﹣2+c,解得c=2,
∴B(0,2),
∵拋物線y=﹣ ![]() x2+bx+c經過點A,B,
x2+bx+c經過點A,B,
∴ ![]() ,解得
,解得 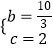 ,
,
∴拋物線解析式為y=﹣ ![]() x2+
x2+ ![]() x+2
x+2
(2)
解:①由(1)可知直線解析式為y=﹣ ![]() x+2,
x+2,
∵M(m,0)為x軸上一動點,過點M且垂直于x軸的直線與直線AB及拋物線分別交于點P,N,
∴P(m,﹣ ![]() m+2),N(m,﹣
m+2),N(m,﹣ ![]() m2+
m2+ ![]() m+2),
m+2),
∴PM=﹣ ![]() m+2,PA=3﹣m,PN=﹣
m+2,PA=3﹣m,PN=﹣ ![]() m2+
m2+ ![]() m+2﹣(﹣
m+2﹣(﹣ ![]() m+2)=﹣
m+2)=﹣ ![]() m2+4m,
m2+4m,
∵△BPN和△APM相似,且∠BPN=∠APM,
∴∠BNP=∠AMP=90°或∠NBP=∠AMP=90°,
當∠BNP=90°時,則有BN⊥MN,
∴BN=OM=m,
∴ ![]() =
= ![]() ,即
,即 ![]() =
=  ,解得m=0(舍去)或m=2,
,解得m=0(舍去)或m=2,
∴M(2,0);
當∠NBP=90°時,則有 ![]() =
= ![]() ,
,
∵A(3,0),B(0,2),P(m,﹣ ![]() m+2),
m+2),
∴BP= ![]() =
= ![]() m,AP=
m,AP= ![]() =
= ![]() (3﹣m),
(3﹣m),
∴ 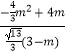 =
= 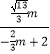 ,解得m=0(舍去)或m=
,解得m=0(舍去)或m= ![]() ,
,
∴M( ![]() ,0);
,0);
綜上可知當以B,P,N為頂點的三角形與△APM相似時,點M的坐標為(2,0)或( ![]() ,0);
,0);
②由①可知M(m,0),P(m,﹣ ![]() m+2),N(m,﹣
m+2),N(m,﹣ ![]() m2+
m2+ ![]() m+2),
m+2),
∵M,P,N三點為“共諧點”,
∴有P為線段MN的中點、M為線段PN的中點或N為線段PM的中點,
當P為線段MN的中點時,則有2(﹣ ![]() m+2)=﹣
m+2)=﹣ ![]() m2+
m2+ ![]() m+2,解得m=3(三點重合,舍去)或m=
m+2,解得m=3(三點重合,舍去)或m= ![]() ;
;
當M為線段PN的中點時,則有﹣ ![]() m+2+(﹣
m+2+(﹣ ![]() m2+
m2+ ![]() m+2)=0,解得m=3(舍去)或m=﹣1;
m+2)=0,解得m=3(舍去)或m=﹣1;
當N為線段PM的中點時,則有﹣ ![]() m+2=2(﹣
m+2=2(﹣ ![]() m2+
m2+ ![]() m+2),解得m=3(舍去)或m=﹣
m+2),解得m=3(舍去)或m=﹣ ![]() ;
;
綜上可知當M,P,N三點成為“共諧點”時m的值為 ![]() 或﹣1或﹣
或﹣1或﹣ ![]()
【解析】(1)把A點坐標代入直線解析式可求得c,則可求得B點坐標,由A、B的坐標,利用待定系數法可求得拋物線解析式;(2)①由M點坐標可表示P、N的坐標,從而可表示出MA、MP、PN、PB的長,分∠NBP=90°和∠BNP=90°兩種情況,分別利用相似三角形的性質可得到關于m的方程,可求得m的值;②用m可表示出M、P、N的坐標,由題意可知有P為線段MN的中點、M為線段PN的中點或N為線段PM的中點,可分別得到關于m的方程,可求得m的值.
【考點精析】關于本題考查的線段的中點和相似三角形的判定與性質,需要了解線段的中點到兩端點的距離相等;相似三角形的一切對應線段(對應高、對應中線、對應角平分線、外接圓半徑、內切圓半徑等)的比等于相似比;相似三角形周長的比等于相似比;相似三角形面積的比等于相似比的平方才能得出正確答案.


 優翼小幫手同步口算系列答案
優翼小幫手同步口算系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠B>∠C,AD⊥BC,垂足為D,AE平分∠BAC.
(1)已知∠B=60°,∠C=30°,求∠DAE的度數;
(2)已知∠B=3∠C,求證:∠DAE=∠C.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線 ![]() 與x軸的負半軸交于點A,與y軸交于點B,連結AB.點C
與x軸的負半軸交于點A,與y軸交于點B,連結AB.點C ![]() 在拋物線上,直線AC與y軸交于點D.
在拋物線上,直線AC與y軸交于點D.
(1)求c的值及直線AC的函數表達式;
(2)點P在x軸的正半軸上,點Q在y軸正半軸上,連結PQ與直線AC交于點M,連結MO并延長交AB于點N,若M為PQ的中點.
①求證:△APM∽△AON;
②設點M的橫坐標為m , 求AN的長(用含m的代數式表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系中,已知拋物線y=ax2+bx﹣5與x軸交于A(﹣1,0),B(5,0)兩點,與y軸交于點C.
(1)求拋物線的函數表達式;
(2)若點D是y軸上的一點,且以B,C,D為頂點的三角形與△ABC相似,求點D的坐標;
(3)如圖2,CE∥x軸與拋物線相交于點E,點H是直線CE下方拋物線上的動點,過點H且與y軸平行的直線與BC,CE分別交于點F,G,試探究當點H運動到何處時,四邊形CHEF的面積最大,求點H的坐標及最大面積;
(4)若點K為拋物線的頂點,點M(4,m)是該拋物線上的一點,在x軸,y軸上分別找點P,Q,使四邊形PQKM的周長最小,求出點P,Q的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC 中,點 D 是邊 BC 上的點(與 B、C 兩點不重合),過點 D作 DE∥AC,DF∥AB,分別交 AB、AC 于 E、F 兩點,下列說法正確的是( )
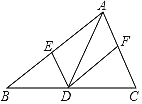
A. 若 AD 平分∠BAC,則四邊形 AEDF 是菱形
B. 若 BD=CD,則四邊形 AEDF 是菱形
C. 若 AD 垂直平分 BC,則四邊形 AEDF 是矩形
D. 若 AD⊥BC,則四邊形 AEDF 是矩形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列等式:
①3-2![]() =(
=(![]() -1)2;
-1)2;
②5-2![]() =(
=(![]() -
-![]() )2;
)2;
③7-2![]() =(
=(![]() -
-![]() )2;…
)2;…
(1)請你根據以上規律,寫出第6個等式 .
(2)第n個等式可以表示為 ,并請你證明你得到的等式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在7×7網格中,每個小正方形邊長都為1.建立適當的平面直角坐標系,使點A(3,4)、C(4,2).

(1)判斷△ABC的形狀,并求圖中格點△ABC的面積;
(2)在x軸上有一點P,使得PA+PC最小,則PA+PC的最小值為__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com