
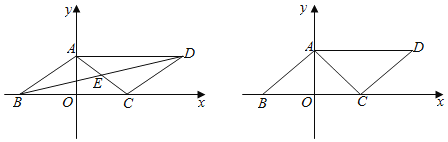
【題目】如圖,已知□ABCD邊BC在x軸上,頂點A在y軸上,對角線AC所在的直線為y=![]() +6,且AC=AB,若點P從點A出發以1cm/s的速度向終點O運動,同時點Q從點C出發以2cm/s的速度沿射線CB運動,當點P到達終點O時,點Q也隨之停止運動.設點P的運動時間為t(s).
+6,且AC=AB,若點P從點A出發以1cm/s的速度向終點O運動,同時點Q從點C出發以2cm/s的速度沿射線CB運動,當點P到達終點O時,點Q也隨之停止運動.設點P的運動時間為t(s).
(1)直接寫出頂點D的坐標(______,______),對角線的交點E的坐標(______,______);
(2)求對角線BD的長;
(3)是否存在t,使S△POQ=![]() SABCD,若存在,請求出的t值;不存在說明理由.
SABCD,若存在,請求出的t值;不存在說明理由.
(4)在整個運動過程中,PQ的中點到原點O的最短距離是______cm,(直接寫出答案)
【答案】(1)16;6;4;3;(2)BD=6![]() ;(3)存在,t值為2;(4)此時PQ的中點到原點O的最短距離為
;(3)存在,t值為2;(4)此時PQ的中點到原點O的最短距離為![]() .
.
【解析】
(1)令x=0,y=0代入解析式得出A,C坐標,進而利用平行四邊形的性質解答即可;
(2)根據平行四邊形的性質得出點B,D坐標,利用兩點間距離解答即可;
(3)利用三角形的面積公式和平行四邊形的面積公式列出方程解答即可;
(4)根據直角三角形斜邊上中線等于斜邊的一半可知,當PQ長度最短時,PQ的中點到原點O的距離最短解答即可.
(1)把x=0代入y=![]() +6,可得y=6,
+6,可得y=6,
即A的坐標為(0,6),
把y=0代入y=![]() +6,可得:x=8,
+6,可得:x=8,
即點C的坐標為(8,0),
根據平行四邊形的性質可得:點B坐標為(-8,0),
所以AD=BC=16,
所以點D坐標為(16,6),
點E為對角線的交點,
故點E是AC的中點,
E的坐標為(4,3),
故答案為:16;6;4;3;
(2)因為B(-8,0)和D(16,6),
∴BD=![]() ;
;
(3)設時間為t,可得:OP=6-t,OQ=8-2t,
∵S△POQ= SABCD,
當0<t≤4時,![]() ,
,
解得:t1=2,t2=8(不合題意,舍去),
當4<t≤6時,![]() ,
,
△<0,不存在,
答:存在S△POQ=![]() SABCD,此時t值為2;
SABCD,此時t值為2;
(4)∵![]() ,
,
當t=![]() 時,PQ=
時,PQ=![]() ,
,
當PQ長度最短時,PQ的中點到原點O的距離最短,此時PQ的中點到原點O的最短距離為![]() PQ=
PQ=![]()
![]() =
=![]()


 走進文言文系列答案
走進文言文系列答案科目:初中數學 來源: 題型:
【題目】先化簡,再求值.
(1)6a2-5a(a+2b-1)+a(-a+10b)+5,其中a=-1,b=2008;
(2)3xy2﹣[xy﹣2(2xy﹣![]() x2y)+2xy2]+3x2y,其中x、y滿足(x+2)2+|y﹣1|=0.
x2y)+2xy2]+3x2y,其中x、y滿足(x+2)2+|y﹣1|=0.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】國家自2016年1月1日起實行全面放開二胎政策,某計生組織為了解該市家庭對待這項政策的態度,準備采用以下調查方式中的一種進行調查:
A.從一個社區隨機選取1 000戶家庭調查;
B.從一個城鎮的不同住宅樓中隨機選取1 000戶家庭調查;
C.從該市公安局戶籍管理處隨機抽取1 000戶城鄉家庭調查.
(1)在上述調查方式中,你認為比較合理的一個是【1】.(填“A”、“B”或“C”)
(2)將一種比較合理的調查方式調查得到的結果分為四類:(A)已有兩個孩子;
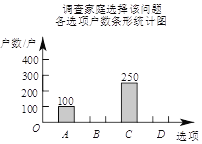
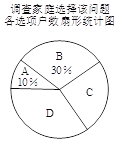
(B)決定生二胎;(C)考慮之中;(D)決定不生二胎.將調查結果繪制成如下兩幅不完整的統計圖.
請根據以上不完整的統計圖提供的信息,解答下列問題:
①補全條形統計圖.
②估計該市100萬戶家庭中決定不生二胎的家庭數.
查看答案和解析>>
科目:初中數學 來源: 題型:
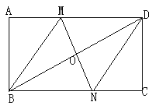
【題目】如圖,在矩形ABCD中,對角線BD的垂直平分線MN與AD相交于點N,連接BM,DN.
(1)求證:四邊形BMDN是菱形;
(2)若AB=4,AD=8,求MD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
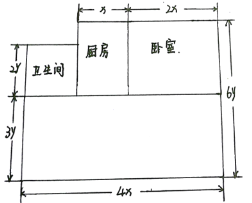
【題目】如圖是一套房子的平面圖,尺寸如圖.
(1)這套房子的總面積是多少?(用含x、y的代數式表示)
(2)如果x=1.8米,y=1米,那么房子的面積是多少平方米?如果每平方米房價為5萬元,那么房屋總價多少萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,點D.E分別在邊AB,AC上,DE∥BC,按下列要求畫圖并填空
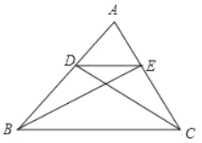
(1)過點E畫直線BC的垂線交直線BC于點F;
(2)點D到直線______的距離等于線段EF的長度
(3)聯結BE.CD,EBC的面積______DBC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某班同學為了解2019年某小區家庭月均用水情況,隨機調查了該小區部分家庭,并將調查數據進行整理如下:
月均用水量x(t) | 頻數(戶) | 頻率 |
| 6 | 0.12 |
| 0.24 | |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | |
| 2 | 0.04 |

請解答下列問題:
(1)把上面的頻數分布表和頻數分布直方圖補充完整;
(2)求該小區用水量不超過15t的家庭占被調查家庭總數的百分比;
(3)若該小區有1000戶家庭,根據調查數據估計,該小區月均用水量超過20t的家庭大約有多少戶?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】星期五晚上,小明和他的媽媽一起看《歌手》,歌手演唱完后要評選出名次,在已公布四到七名后,還有華晨宇、汪峰、張韶涵三位選手沒有公布名次.
(1)求汪峰獲第一名的概率;
(2)如果小明和媽媽一起競猜第一名,那么兩人中一個人猜中另一個人卻沒猜中的概率是多少?(請用“樹狀圖”或“列表”等方法寫出分析過程)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)圖(1)是一個長為2m,寬為2n的矩形,把此矩形沿圖中虛線用剪刀均分為四個小長方形,然后按圖(2)的形狀拼成一個大正方形.請問:這兩個圖形的什么量不變?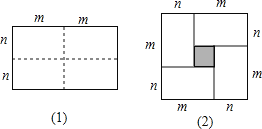
(2)把所得的大正方形面積比原矩形的面積多出的陰影部分的面積用含m,n的代數式表示為(m-n)2或m2-2mn+n2 .
(3)由前面的探索可得出的結論是:在周長一定的矩形中,當 時,面積最大.
(4)若矩形的周長為24cm,則當邊長為多少時,該圖形的面積最大?最大面積是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com