
 x+3的圖象與x軸交于點A,與y軸交于點B,動點P從點B出發沿BA向終點A運動,同時動點Q從點O出發沿OB向點B運動,到達點B后立刻以原來的速度沿BO返回.點P,Q運動速度均為每秒1個單位長度,當點P到達點A時停止運動,點Q也同時停止.連結PQ,設運動時間為t(t>0)秒.
x+3的圖象與x軸交于點A,與y軸交于點B,動點P從點B出發沿BA向終點A運動,同時動點Q從點O出發沿OB向點B運動,到達點B后立刻以原來的速度沿BO返回.點P,Q運動速度均為每秒1個單位長度,當點P到達點A時停止運動,點Q也同時停止.連結PQ,設運動時間為t(t>0)秒.
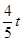 ,﹣
,﹣ x+3);
x+3);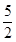 或
或 時,O在l的垂直平分線上.
時,O在l的垂直平分線上.
 x+3的圖象與x軸交于點A,與y軸交于點B
x+3的圖象與x軸交于點A,與y軸交于點B ,
, ,
, .
.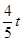 代入y=﹣
代入y=﹣ x+3,得y=﹣
x+3,得y=﹣ x+3,
x+3,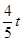 ,﹣
,﹣ x+3);
x+3); OA·OB=
OA·OB= =6,
=6,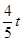 ,﹣
,﹣ x+3),
x+3),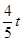 ,PC=﹣
,PC=﹣ x+3,
x+3,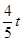 )2+(﹣
)2+(﹣ x+3)2,
x+3)2,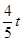 )2+(﹣
)2+(﹣ t+3)2,解得 t=
t+3)2,解得 t=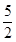 ,符合要求.
,符合要求.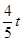 )2+(﹣
)2+(﹣ t+3)2
t+3)2 ,符合要求.
,符合要求.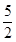 或
或 時,O在l的垂直平分線上.
時,O在l的垂直平分線上.

科目:初中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 x+b,求n的值.
x+b,求n的值.查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
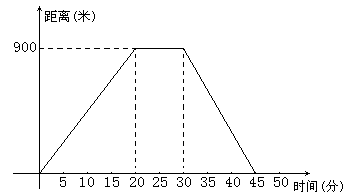
 兩地同時出發相向而行,其中甲到
兩地同時出發相向而行,其中甲到 地后立即返回,下圖是它們離各自出發地的距離
地后立即返回,下圖是它們離各自出發地的距離 (千米)與行駛時間
(千米)與行駛時間 (小時)之間的函數圖象.
(小時)之間的函數圖象. (千米)與行駛時間
(千米)與行駛時間 (小時)之間的函數關系式,并寫出自變量的取值范圍;
(小時)之間的函數關系式,并寫出自變量的取值范圍; 小時,求乙車離出發地的距離
小時,求乙車離出發地的距離 (千米)與行駛時間
(千米)與行駛時間 (小時)之間的函數關系式;
(小時)之間的函數關系式;
查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題
A. | B. | C. | D. |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com