
【題目】如圖,拋物線C1:y=x2﹣2x與拋物線C2:y=ax2+bx開口大小相同、方向相反,它們相交于O,C兩點,且分別與x軸的正半軸交于點B,點A,OA=2OB.
(1)求拋物線C2的解析式;
(2)在拋物線C2的對稱軸上是否存在點P,使PA+PC的值最小?若存在,求出點P的坐標,若不存在,說明理由;
(3)M是直線OC上方拋物線C2上的一個動點,連接MO,MC,M運動到什么位置時,△MOC面積最大?并求出最大面積.

【答案】(1)y=﹣x2+4x;(2)線段OC的長度![]() ;(3)S△MOC最大值為
;(3)S△MOC最大值為![]() .
.
【解析】
(1)C1、C2:y=ax2+bx開口大小相同、方向相反,則a=-1,將點A的坐標代入C2的表達式,即可求解;
(2)點A關于C2對稱軸的對稱點是點O(0,0),連接OC交函數C2的對稱軸與點P,此時PA+PC的值最小,即可求解;
(3)S△MOC=![]() MH×xC=
MH×xC=![]() (-x2+4x-x)= -
(-x2+4x-x)= -![]() x2+
x2+![]() x,即可求解.
x,即可求解.
(1)令:y=x2﹣2x=0,則x=0或2,即點B(2,0),
∵C1、C2:y=ax2+bx開口大小相同、方向相反,則a=﹣1,
則點A(4,0),將點A的坐標代入C2的表達式得:
0=﹣16+4b,解得:b=4,
故拋物線C2的解析式為:y=﹣x2+4x;
(2)聯立C1、C2表達式并解得:x=0或3,
故點C(3,3),
連接OC交函數C2的對稱軸與點P,
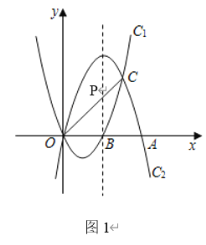
此時PA+PC的值最小為:線OC的長度![]() ;
;
設OC所在直線方程為:![]()
將點O(0,0),C(3,3)帶入方程,解得k=1,
所以OC所在直線方程為:![]()
![]() 點P在函數C2的對稱軸上,令x=2,帶入直線方程得y=2,
點P在函數C2的對稱軸上,令x=2,帶入直線方程得y=2,
![]() 點P坐標為(2,2)
點P坐標為(2,2)
(3)由(2)知OC所在直線的表達式為:y=x,
過點M作y軸的平行線交OC于點H,
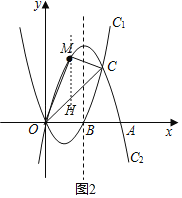
設點M(x,﹣x2+4x),則點H(x,x),則MH=﹣x2+4x﹣x
則S△MOC=S△MOH+S△MCH
=![]() MH×xC =
MH×xC = ![]() (﹣x2+4x﹣x)=
(﹣x2+4x﹣x)=![]()
∵△MOC的面積是一個關于x的二次函數,且開口向下
![]() 其頂點就是它的最大值。其對稱軸為x=
其頂點就是它的最大值。其對稱軸為x=![]() =
=![]() ,此時y=
,此時y=![]()
S△MOC最大值為![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】廣宇、承義兩名同學分別進行5次射擊訓練,訓練成績(單位:環)如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
廣宇 | 9 | 8 | 7 | 7 | 9 |
承義 | 6 | 8 | 10 | 8 | 8 |
對他們的訓練成績作如下分析,其中說法正確的是( )
A.廣宇訓練成績的平均數大于承義訓練成績平均數
B.廣宇訓練成績的中位數與承義訓練成績中位數不同
C.廣宇訓練成績的眾數與承義訓練成績眾數相同
D.廣宇訓練成績比承義訓練成績更加穩定
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】假設某商場地下停車場有5個出入口,每天早晨7點開始對外停車且此時車位空置率為90%,在每個出入口的車輛數均是勻速出入的情況下,如果開放2個進口和3個出口,6小時車庫恰好停滿;如果開放3個進口和2個出口,3小時車庫恰好停滿.2019年清明節期間,由于商場人數增多,早晨7點時的車位空置率變為60%,因為車庫改造,只能開放1個進口和1個出口,則從早晨7點開始經過______小時車庫恰好停滿.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是二次函數y=ax2+bx+c(a,b,c是常數,a≠0)圖象的一部分,與x軸的交點A在點(2,0)和(3,0)之間,對稱軸是x=1.對于下列說法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m為實數);⑤當﹣1<x<3時,y>0,其中正確的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了了解學生參加體育活動的情況,學校對學生進行隨機抽樣調查,其中一個問題是“你平均每天參加體育活動的時間是多少”,共有4個選項:A 1.5小時以上;B 1~1.5小時;C 0.5~1小時;D 0.5小時以下.圖1、2是根據調查結果繪制的兩幅不完整的統計圖,請你根據統計圖提供的信息,解答以下問題:

(1)本次一共調查了多少名學生?
(2)在圖1中將選項B的部分補充完整;
(3)若該校有3000名學生,你估計全校可能有多少名學生平均每天參加體育活動的時間在0.5小時以下.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,點E是BC邊的中點,動點M在CD邊上運動,以EM為折痕將△CEM折疊得到△PEM,連接PA,若AB=4,∠BAD=60°,則PA的最小值是_____.
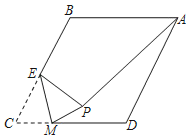
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線![]() 經過
經過![]() ,
,![]() 兩點,與x軸的另一個交點為C,頂點為D,連結CD.
兩點,與x軸的另一個交點為C,頂點為D,連結CD.
(1)求該拋物線的表達式;
(2)點P為該拋物線上一動點(與點B、C不重合),設點P的橫坐標為t.
①當點P在直線BC的下方運動時,求![]() 的面積的最大值;
的面積的最大值;
②該拋物線上是否存在點P,使得![]() 若存在,求出所有點P的坐標;若不存在,請說明理由.
若存在,求出所有點P的坐標;若不存在,請說明理由.
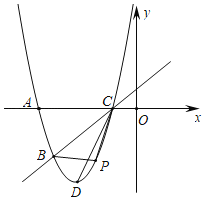
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,函數y=![]() (k>0,x>0)的圖象與等邊三角形OAB的邊OA,AB分別交于點M,N,且OM=2MA,若AB=3,那么點N的橫坐標為( )
(k>0,x>0)的圖象與等邊三角形OAB的邊OA,AB分別交于點M,N,且OM=2MA,若AB=3,那么點N的橫坐標為( )
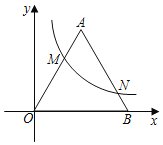
A.![]() B.
B.![]() C.4D.6
C.4D.6
查看答案和解析>>
科目:初中數學 來源: 題型:
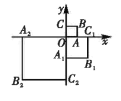
【題目】如圖,在平面直角坐標系![]() 中,正方形
中,正方形![]() 的頂點
的頂點![]() 分別在
分別在![]() ,
,![]() 軸上,且
軸上,且![]() .將正方形
.將正方形![]() 繞原點
繞原點![]() 順時針旋轉
順時針旋轉![]() ,且
,且![]() ,得到正方形
,得到正方形![]() ,再將正方
,再將正方![]() 繞原點
繞原點![]() 順時針旋轉
順時針旋轉![]() ,且
,且![]() ,得到正方形
,得到正方形![]() ,以此規律,得到正方形
,以此規律,得到正方形![]() ,則點
,則點![]() 的坐標為__________.
的坐標為__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com