Question

【題目】Rt△ABC中，∠B=90°∠A=30°．以C為圓心，小于BC長為半徑畫弧與AC、BC邊交于點F、E．分別以E、F為圓心，大于EF為半徑畫弧，兩弧交于點N，若BC= ， 則點M到AC的距離是（　　）

A.1
B.
C.
D.3

Answer 1

【答案】A
【解析】解：∵在Rt△ABC中，∠B=90°∠A=30°，
∴∠ACB=60°，
∵以C為圓心，小于BC長為半徑畫弧與AC、BC邊交于點F、E．分別以E、F為圓心，大于EF為半徑畫弧，兩弧交于點N，
∴∠ACM=∠MCB=30°，
∵∠B=90°，
∴CM=2BM，
∵BC= ，
∴由勾股定理得：BM2+（）2=（2BM）2 ，
解得：BM=1，
∵∠B=90°，∠ACM=∠BCM，
∴點M到AC的距離等于BM的長，即是1，
故選A．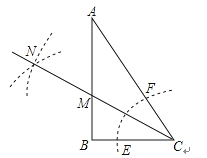

【考點精析】關于本題考查的角平分線的性質定理，需要了解定理1：在角的平分線上的點到這個角的兩邊的距離相等； 定理2：一個角的兩邊的距離相等的點，在這個角的平分線上才能得出正確答案．