【題目】某地的一座人行天橋如圖所示，天橋高為6米，坡面BC的坡度為1：1，為了方便行人推車過天橋，有關部門決定降低坡度，使新坡面的坡度為1：
．
（1）求新坡面的坡角∠CAB的度數；
（2）原天橋底部正前方8米處（PB的長）的文化墻PM是否需要拆除？請說明理由．
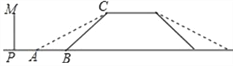
【答案】（1）新坡面的坡角為30°；（2）文化墻PM不需要拆除．
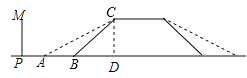
【解析】試題分析：（1）由新坡面的坡度為1：
，由特殊角的三角函數值，即可求得新坡面的坡角；（2）過點C作CD⊥AB于點D，由坡面BC的坡度為1：1，新坡面的坡度為1：．即可求得AD，BD的長，繼而求得AB的長，則可求得答案．
試題解析：（1）∵新坡面的坡度為1：，
∴tanα=tan∠CAB=
=
，
∴∠α=30°．
答：新坡面的坡角a為30°；
（2）文化墻PM不需要拆除．
過點C作CD⊥AB于點D，則CD=6，
∵坡面BC的坡度為1：1，新坡面的坡度為1：，
∴BD=CD=6，AD=6，
∴AB=AD﹣BD=6﹣6＜8，
∴文化墻PM不需要拆除．
科目：初中數學 來源： 題型：
【題目】我們學過角的平分線的概念．類比給出新概念：從一個角的頂點出發，把這個角分成
的兩個角的射線，叫做這個角的三分線．顯然，一個角的三分線有兩條，例如：如圖1，若
，則
是
的一條三分線．
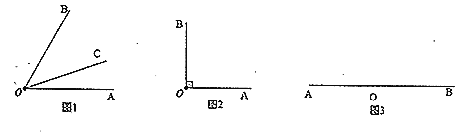
（1）如圖1，若
，若
，求
的度數；
（2）如圖2，若
，若
是的兩條三分線．
①求
的度數；
②現以O為中心，將順時針旋轉
度（
）得到
，當
恰好是的三分線時，則求的值．
（3）如圖3，若
，是的一條三分線，
分別是與
的平分線，將
繞點
以每秒
的速度沿順時針方向旋轉一周，在旋轉的過程中，若射線
恰好是的三分線，則此時繞點旋轉的時間是多少秒？（直接寫出答案即可，不必說明理由）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】定義：如果10b＝n，那么稱b為n的勞格數，記為b＝d（n）．
（1）根據勞格數的定義，可知：d（10）＝1，d（102）＝2,那么：d（103）＝ ．
（2）勞格數有如下運算性質：若m，n為正數，則d（mn）＝d（m）+d（n）； d（
）＝d（m）﹣d（n）．若d（3）＝0.48，d（2）＝0.3，根據運算性質，填空：d（6）＝ ，則d（
）＝ ，d（
）＝ ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下面表格給出了直線
上部分點（x，y）的坐標值．
x | -2 | 0 | 2 | 4 |
y | 3 | 1 | -1 | -3 |
（1）直線與
軸的交點坐標是___________；
（2）直線與兩坐標軸圍成的三角形的面積等于___________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】有個填寫運算符號的游戲：在“
”中的每個□內，填入
中的某一個（可重復使用），然后計算結果．
（1）計算：
；
（2）若請推算
□內的符號；
（3）在“
”的□內填入符號后，使計算所得數最小，直接寫出這個最小數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】全民健身運動已成為一種時尚 ，為了解揭陽市居民健身運動的情況，某健身館的工作人員開展了一項問卷調查，問卷內容包括五個項目:
A:健身房運動；B:跳廣場舞；C:參加暴走團；D:散步；E:不運動.
以下是根據調查結果繪制的統計圖表的一部分，
運動形式 | A | B | C | D | E |
人數 |
|
|
|
|
|
請你根據以上信息，回答下列問題:
接受問卷調查的共有 人，圖表中的
，
.
統計圖中，
類所對應的扇形的圓心角的度數是 度.
揭陽市環島路是市民喜愛的運動場所之一，每天都有“暴走團”活動，若某社區約有
人，請你估計一下該社區參加環島路“暴走團”的人數.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某人準備購買一套小戶型住房，他去某樓盤了解情況得知，該戶型單價是
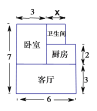
元/
，總面積如圖所示（單位：米，衛生間的寬未定，設寬為
米），售房部為他提供了以下兩種優惠方案： 方案一：需購買全部總面積，但整套房按原銷售總金額的9折出售；
方案二：整套房的單價仍是12000元/，但不需要購買全部面積，其中，只對廚房面積進行了優惠，只算廚房
的面積，其余房間面積不變．
（1）求衛生間的面積；
（2）請分別求出兩種方案購買一套該戶型商品房的總金額；
（3）當1≤≤2，且為整數時，選哪種方案購買一套該戶型商品房的總金額較少？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
