
【題目】如圖,點A從原點出發沿數軸向左運動,同時,點B也從原點出發沿數軸向右運動,3s后,兩點相距18個單位長度.已知點B的速度是點A的速度的5倍(速度單位:單位長度/s).
(1)求出點A、點B運動的速度,并在數軸上標出A,B兩點從原點出發運動3s時的位置;
(2)若A,B兩點從(1)中的位置開始,仍以原來的速度同時沿數軸向左運動,幾秒時,原點恰好處在點A、點B的正中間?
(3)當A,B兩點從(2)中的位置繼續以原來的速度沿數軸向左運動的同時,另一點C從原點位置也向點A運動,當遇到點A后,立即返回向點B運動,遇到點B后又立即返回向點A運動,如此往返,直到點B追上點A時,點C立即停止運動.若點C一直以8個單位長度/s的速度勻速運動,則點C從開始運動到停止運動,行駛的路程是多少個單位長度?

【答案】(1)點A的速度為每秒1個單位長度,則點B的速度為每秒5個單位長度,圖見解析;
(2)2秒時,原點恰好處在點A、點B的正中間;
(3)C行駛的路程為20個單位長度.
【解析】試題分析:(1)設點A的速度為每秒t個單位,則點B的速度為每秒5t個單位,由甲的路程+乙的路程=總路程建立方程求出其解即可;
(2)設x秒時原點恰好處在點A、點B的正中間,根據兩點離原點的距離相等建立方程求出其解即可;
(3)先根據追擊問題求出A、B相遇的時間就可以求出C行駛的路程.
試題解析:(1)設點A的速度為每秒t個單位,則點B的速度為每秒5t個單位,由題意,得:
3t+3×5t=18,
解得:t=1,
∴點A的速度為每秒1個單位長度,則點B的速度為每秒5個單位長度.
如圖:
![]()
(2)設x秒時原點恰好在A、B的中間,由題意,得
3+x=15-5x,
解得:x=2.
∴2秒時,原點恰好處在點A、點B的正中間;
(3)由題意,得
B追上A的時間為:10÷(5-1)=2.5秒,
∴C行駛的路程為:2.5×10=25個單位長度.


科目:初中數學 來源: 題型:
【題目】某地的一種綠色蔬菜,在市場上若直接銷售,每噸利潤為1000元,經粗加工后銷售,每噸利潤4000元,經精加工后銷售, 每噸利潤為7000元.當地一家公司現有這種蔬菜140噸,該公司加工廠的生產能力是:如果對蔬菜進行粗加工,每天可加工16噸, 如果對蔬菜進行精加工,每天可加工6噸,但每天兩種方式不能同時進行.受季節等條件的限制,必須用15天時間將這批蔬菜全部銷售或加工完畢.為此,公司研制了三種方案:
方案1:將蔬菜全部進行粗加工;
方案2:盡可能地對蔬菜進行精加工,沒來得及加工的蔬菜,在市場上直接出售;
方案3:將一部分蔬菜進行精加工, 其余蔬菜進行粗加工,并剛好15天完成.
如果你是公司經理,你會選擇哪一種方案? 請通過計算說明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2018年體育中考中,我班一學習小組6名學生的體育成績如下表,則這組學生的體育成績的眾數,中位數依次為( )
成績(分) | 47 | 48 | 50 |
人數 | 2 | 3 | 1 |
A. 48,48 B. 48,47.5 C. 3,2.5 D. 3,2
查看答案和解析>>
科目:初中數學 來源: 題型:
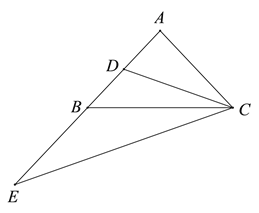
【題目】如圖,在△ABC中,AB=AC,CD是AB邊上的中線,延長AB至點E,使BE=AB,連接CE. 請你探究:
(1)當∠BAC為直角時,直接寫出線段CE與CD之間的數量關系;
(2)當∠BAC為銳角或鈍角時,(1)中的上述數量關系是否仍然成立?若成立,請給出證明;若不成立,請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題正確的是( )
A.有一組鄰邊相等的平行四邊形是正方形
B.有一個角是直角的平行四邊形是正方形
C.對角線相等的菱形是正方形
D.對角線互相平分的矩形是正方形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC,則下面結論錯誤的是( ) 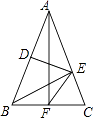
A.BF=EF
B.DE=EF
C.∠EFC=45°
D.∠BEF=∠CBE
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學規定學生的學期體育成績滿分為100分,其中課外體育占20%,期中考試成績占30%,期末考試成績占50%.小彤的三項成績(百分制)依次為95、90、88,則小彤這學期的體育成績為( )
A. 89 B. 90 C. 92 D. 93
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com