Question

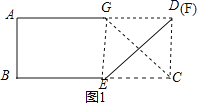
【題目】如圖，在矩形紙片中，，折疊紙片，使點剛好落在線段上，且折痕分別于相交，設折疊后點的對應點分別為點，折痕分別于相交于點，則線段的取值范圍是__________.

Answer 1

【答案】

【解析】

由四邊形ABCD是矩形，根據折疊的性質，易證得△EFG是等腰三角形，即可得GF=EC，又由GF∥EC，即可得四邊形CEGF為平行四邊形，根據鄰邊相等的平行四邊形是菱形，即可得四邊形BGEF為菱形，如圖2，當G與A重合時，CE取最大值，由折疊的性質得CD=DG，∠CDE=∠GDE=45°，推出四邊形CEGD是矩形，根據矩形的性質即可得到CE=CD=AB=3；如圖1，當F與D重合時，CE取最小值，由折疊的性質得AE=CE，根據勾股定理即可得到結論．

證明：∵四邊形ABCD是矩形，

∴AD∥BC，
∴∠GFE=∠FEC，
∵圖形翻折后點G與點C重合，EF為折線，
∴∠GEF=∠FEC，
∴∠GFE=∠FEG，
∴GF=GE，
∵圖形翻折后BC與GE完全重合，
∴BE=EC，

∴GF=EC，
∴四邊形CEGF為平行四邊形，
∴四邊形CEGF為菱形；
∴CE=CD=AB=3；
如圖2，當G與A重合時，CE取最大值，
由折疊的性質得AE=CE，
∵∠B=90°，
∴AE2=AB2+BE2，即CE2=32+（9-CE）2，
∴CE=5，
∴線段CE的取值范圍3≤CE≤5．

故答案為：3≤CE≤5．