
【題目】如圖1,在四邊形![]() 中,
中,![]() ,點
,點![]() 在
在![]() 邊上,
邊上,![]() 平分
平分![]() ,且
,且![]() .
.

(1)求證:![]() ;
;
(2)如圖2,已知![]() 交
交![]() 邊于點
邊于點![]() ,交
,交![]() 邊的延長線于點
邊的延長線于點![]() ,且
,且![]() 平分
平分![]() . 若
. 若![]() ,試比較
,試比較![]() 與
與![]() 的大小,并說明理由.
的大小,并說明理由.
【答案】(1)詳見解析;(2)![]() ,理由詳見解析.
,理由詳見解析.
【解析】
(1)根據角平分線的定義可得∠CDE=∠ADE,再結合已知條件可得∠CDE=∠DEA,從而得出CD∥AB,根據平行線的性質以及已知條件可得∠B+∠A=180°,從而證得AD∥BC;
(2)由垂直的定義可得∠BGF=90°,由AD∥BC可得∠ADF=∠BGF=90°,由CD∥AB可得∠CDF=∠F,設∠EDB=∠BDF=x°,∠CDF=∠F=y°,則∠EDF=2x°,∠ADE=∠EDC=(2x+y)°,由∠ADF=∠ADE+∠EDF,得2x+y+2x=90,得出y=90-4x,∠F=∠EDF=y°-2x°=90°-6x°,再根據∠BDC<45°得出x+y<45°,求出x的取值范圍,進而比較出∠F與∠EDF的大小.
(1)證明:
∵![]() 平分
平分![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∴![]()
∴![]()
又∵![]() ,
,
∴![]() .
.
∴![]() .
.
(2)解:
∵![]() ,
,
∴![]() .
.
又∵![]()
∴![]()
∵![]() ,
,
∴![]() .
.
設![]() ,
,![]()
則![]() ,
,![]()
由![]() ,得
,得
![]()
∴![]()
∴![]()
![]()
![]()
![]()
∵![]()
∴![]()
![]() ,
,
解得,![]()
∴![]() .
.
∴![]()
![]()
∴![]() .
.


科目:初中數學 來源: 題型:
【題目】西南大學附中初2020級小李同學想利用學過的知識測量棵樹的高度,假設樹是豎直生長的,用圖中線段AB表示,小李站在C點測得∠BCA=45°,小李從C點走4米到達了斜坡DE的底端D點,并測得∠CDE=150°,從D點上斜坡走了8米到達E點,測得∠AED=60°,B,C,D在同一水平線上,A、B、C、D、E在同一平面內,則大樹AB的高度約為( )米.(結果精確到0.1米,參考數據:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

A.24.3B.24.4C.20.3D.20.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD的外側作等腰△ABE,AE=BE,連接ED、EC.

(1)求證:ED=EC.
(2)用無刻度的直尺作出△EDC中DC邊上的高EH.(不寫作法,保留作圖的痕跡)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,過邊長為 1 的等邊△ABC 的邊 AB 上一點 P,作 PE⊥AC 于 E,Q 為 BC 延長線上一點,當 PA=CQ 時,連PQ 交 AC 邊于 D,則 DE 的長為( )

A.0.5B.1C.0.25D.2
查看答案和解析>>
科目:初中數學 來源: 題型:
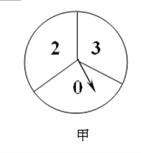
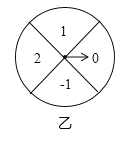
【題目】如圖,甲轉盤被分成3個面積相等的扇形,乙轉盤被分成4個面積相等的扇形,每一個扇形都標有相應的數字.同時轉動兩個轉盤,當轉盤停止后,設甲轉盤中指針所指區域內的數字為x,乙轉盤中指針所指區域內的數字為y(當指針指在邊界線上時,重轉一次,直到指針指向一個區域為止).
(1)請你用畫樹狀圖或列表格的方法,列出所有等可能情況,并求出點(x,y)落在坐標軸上的概率;
(2)直接寫出點(x,y)落在以坐標原點為圓心,2為半徑的圓內的概率為_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年我市某公司分兩次采購了一批大蒜,第一次花費40萬元,第二次花費60萬元,已知第一次采購時每噸大蒜的價格比去年的平均價格上漲了500元,第二次采購時每噸大蒜的價格比去年的平均價格下降了500元,第二次采購的數量是第一次采購數量的兩倍.
(1)試問去年每噸大蒜的平均價格是多少元?
(2)該公司可將大蒜加工成蒜粉或蒜片,若單獨加工成蒜粉,每天可加工8噸大蒜,每噸大蒜獲利1000元;若單獨加工成蒜片,每天可加工12噸大蒜,每噸大蒜獲利600元.為出口需要,所有采購的大蒜必須在30天內加工完畢,且加工蒜粉的大蒜數量不少于加工蒜片的大蒜數量的一半.為獲得最大利潤,應將多少噸大蒜加工成蒜粉?最大利潤為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形紙片![]() 中,
中,![]() ,折疊紙片,使點
,折疊紙片,使點![]() 剛好落在線段
剛好落在線段![]() 上,且折痕分別于
上,且折痕分別于![]() 相交,設折疊后點
相交,設折疊后點![]() 的對應點分別為點
的對應點分別為點![]() ,折痕分別于
,折痕分別于![]() 相交于點
相交于點![]() ,則線段
,則線段![]() 的取值范圍是__________.
的取值范圍是__________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】1955年,印度數學家卡普耶卡(![]() )研究了對四位自然數的一種變換:任給出四位數
)研究了對四位自然數的一種變換:任給出四位數![]() ,用
,用![]() 的四個數字由大到小重新排列成一個四位數
的四個數字由大到小重新排列成一個四位數![]() ,再減去它的反序數
,再減去它的反序數![]() (即將
(即將![]() 的四個數字由小到大排列,規定反序后若左邊數字有0,則將0去掉運算,比如0001,計算時按1計算),得出數
的四個數字由小到大排列,規定反序后若左邊數字有0,則將0去掉運算,比如0001,計算時按1計算),得出數![]() ,然后繼續對
,然后繼續對![]() 重復上述變換,得數
重復上述變換,得數![]() ,…,如此進行下去,卡普耶卡發現,無論
,…,如此進行下去,卡普耶卡發現,無論![]() 是多大的四位數,只要四個數字不全相同,最多進行
是多大的四位數,只要四個數字不全相同,最多進行![]() 次上述變換,就會出現變換前后相同的四位數
次上述變換,就會出現變換前后相同的四位數![]() ,這個數稱為
,這個數稱為![]() 變換的核.則四位數9631的
變換的核.則四位數9631的![]() 變換的核為______.
變換的核為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四邊形ABCD中,∠B=∠D=90°,∠C=72°,在BC、CD上分別找一點M、N,使△AMN的周長最小時,∠AMN+∠ANM的度數為_______

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com