
【題目】如圖,已知△ABC是等邊三角形,以AB為直徑作⊙O,交BC邊于點D,交AC邊于點F,作DE⊥AC于點E. 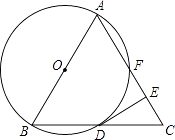
(1)求證:DE是⊙O的切線;
(2)若△ABC的邊長為4,求EF的長度.
【答案】
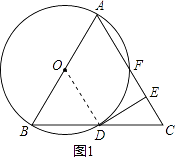
(1)證明:如圖1,連接OD,
∵△ABC是等邊三角形,
∴∠B=∠C=60°.
∵OB=OD,
∴∠ODB=∠B=60°.
∵DE⊥AC,
∴∠DEC=90°.
∴∠EDC=30°.
∴∠ODE=90°.
∴DE⊥OD于點D.
∵點D在⊙O上,
∴DE是⊙O的切線
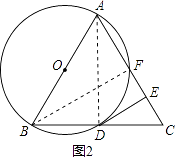
(2)解:如圖2,連接AD,BF,
∵AB為⊙O直徑,
∴∠AFB=∠ADB=90°.
∴AF⊥BF,AD⊥BD.
∵△ABC是等邊三角形,
∴ ![]() ,
, ![]() .
.
∵∠EDC=30°,
∴ ![]() .
.
∴FE=FC﹣EC=1.
【解析】(1)連接OD,根據等邊三角形的性質求出∠ODE=90°,根據切線的判定定理證明即可;(2)連接AD,BF,根據等邊三角形的性質求出DC、CF,根據直角三角形的性質求出EC,結合圖形計算即可.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】已知二次函數的解析式是y=x2﹣2x﹣3
(1)用配方法將y=x2﹣2x﹣3化成y=a(x﹣h)2+k的形式;
(2)在直角坐標系中,用五點法畫出它的圖像; 
(3)利用圖象求當x為何值時,函數值y<0
(4)當x為何值時,y隨x的增大而減小?
(5)當﹣3<x<3時,觀察圖象直接寫出函數值y的取值的范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,AD,BC是⊙O的兩條互相垂直的直徑,點P從點O出發沿圖中某一個扇形順時針勻速運動,設∠APB=y(單位:度),如果y與點P運動的時間x(單位:秒)的函數關系的圖象大致如圖2所示,那么點P的運動路線可能為( )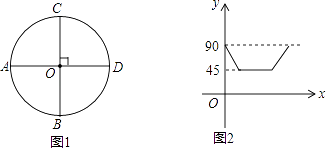
A.O→B→A→O
B.O→A→C→O
C.O→C→D→O
D.O→B→D→O
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了解“課程選修”的情況,對報名參加“藝術鑒賞”,“科技制作”,“數學思維”,“閱讀寫作”這四個選修項目的學生(每人限報一課)進行抽樣調查,下面是根據收集的數據繪制的不完整的統計圖:
請根據圖中提供的信息,解答下面的問題:
(1)此次共調查了___名學生,扇形統計圖中“藝術鑒賞”部分的圓心角是___度;
(2)此次調查“數學思維”的人數為_________,并補充完整條形圖;
(3)現該校共有600名學生報名參加這四個選修項目,請你估計其中有____名學生選修“科技制作”項目.
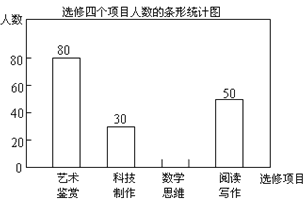
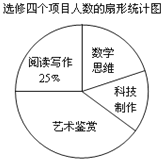
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在平行四邊形ABCD中,點E在邊AD上,以BE為折痕,將△ABE向上翻折,點A正好落在CD上的點F,若△FDE的周長為7,△FCB的周長為19,求FC的長.
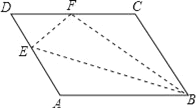
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將正方體骰子(相對面上的點數分別為1和6、2和5、3和4)放置于水平桌面上,如圖1。在圖2中,將骰子向右翻滾90°,然后在桌面上按逆時針方向旋轉90°,則完成一次變換。若骰子的初始位置為圖1所示的狀態,那么按上述規則連續完成14次變換后,骰子朝上一面的點數是_____________________。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】近兩年,國際市場黃金價格漲幅較大,中國交通銀行推出“沃德金”的理財產品,即以黃金為投資產品,投資者從黃金價格的上漲中賺取利潤.上周五黃金的收盤價為![]() 元/克,下表是本周星期一至星期五黃金價格的變化情況.(注:星期一至星期五開市,星期六、星期日休市)
元/克,下表是本周星期一至星期五黃金價格的變化情況.(注:星期一至星期五開市,星期六、星期日休市)
星期 | 一 | 二 | 三 | 四 | 五 |
收盤價的變化(與前一天收盤價比較) |
|
|
|
|
|
問
![]() 本周星期三黃金的收盤價是多少?
本周星期三黃金的收盤價是多少?
![]() 本周黃金收盤時的最高價、最低價分別是多少?
本周黃金收盤時的最高價、最低價分別是多少?
![]() 上周,小王以周五的收盤價
上周,小王以周五的收盤價![]() 元/克買入黃金
元/克買入黃金![]() 克,已知買入與賣出時均需支付成交金額的千分之五的交易費,賣出黃金時需支付成交金額的千分之三的印花稅.本周,小王以周五的收盤價全部賣出黃金
克,已知買入與賣出時均需支付成交金額的千分之五的交易費,賣出黃金時需支付成交金額的千分之三的印花稅.本周,小王以周五的收盤價全部賣出黃金![]() 克,他的收益情況如何?
克,他的收益情況如何?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料,解答問題.
飲水問題是關系到學生身心健康的重要生活環節,東坡中學共有教學班24個,平均每班有學生50人,經估算,學生一年在校時間約為240天(除去各種節假日),春、夏、秋、冬季各60天.原來,學生飲水一般都是購純凈水(其他碳酸飲料或果汁價格更高),純凈水零售價為1.5元/瓶,每個學生春、秋、冬季平均每天買1瓶純凈水,夏季平均每天要買2瓶純凈水,學校為了減輕學生消費負擔,要求每個班自行購買1臺冷熱飲水機,經調查,購買一臺功率為500 W的冷熱飲水機約為150元,純凈水每桶6元,每班春、秋兩季,平均每1.5天購買4桶,夏季平均每天購買5桶,冬季平均每天購買1桶,飲水機每天開10小時,當地民用電價為0.50元/度.
問題:
(1)在未購買飲水機之前,全年平均每個學生要花費多少錢來購買純凈水飲用?
(2)在購買飲水機解決學生飲水問題后,每班當年共要花費多少元?
(3)這項便利學生的措施實施后,東坡中學當年全體學生共節約多少錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:拋物線y=ax2﹣2(a﹣1)x+a﹣2(a>0).
(1)求證:拋物線與x軸有兩個交點;
(2)設拋物線與x軸有兩個交點的橫坐標分別為x1 , x2 , (其中x1>x2).若y是關于a的函數,且y=ax2+x1 , 求這個函數的表達式;
(3)在(2)的條件下,結合函數的圖象回答:若使y≤﹣3a2+1,則自變量a的取值范圍為 . 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com