
【題目】古代阿拉伯數(shù)學家泰比特·伊本·奎拉對勾股定理進行了推廣研究:如圖(圖1中![]() 為銳角,圖2中
為銳角,圖2中![]() 為直角,圖3中
為直角,圖3中![]() 為鈍角).
為鈍角).

在△ABC的邊BC上取![]() ,
, ![]() 兩點,使
兩點,使![]() ,則
,則![]() ∽
∽![]() ∽
∽![]() ,
, ![]() ,
, ![]() ,進而可得
,進而可得![]()
![]() ;(用
;(用![]() 表示)
表示)
若AB=4,AC=3,BC=6,則![]()
![]() .
.
【答案】BC,BC, ![]() ,
, ![]() .
.
【解析】試題分析:
(1)由△ABC∽△B′BA∽△C′AC,可得![]() ,
, ![]() ,由此可得;AB2=B′B·BC,AC2=C′C·BC,由此可得AB2+AC2= B′B·BC+ C′C·BC=BC·(B′B+ C′C);
,由此可得;AB2=B′B·BC,AC2=C′C·BC,由此可得AB2+AC2= B′B·BC+ C′C·BC=BC·(B′B+ C′C);
(2)把AB=4,AC=3,BC=6,代入(1)中所得AB2+AC2= BC·(B′B+ C′C)可解得;B′B+ C′C=![]() ,結合B′B+ C′C=BC+B′C′即可解得:B′C′=
,結合B′B+ C′C=BC+B′C′即可解得:B′C′=![]() .
.
試題分析:
(1)∵△ABC∽△B′BA∽△C′AC,
∴![]() ,
, ![]() ,
,
∴ AB2=B′B·BC,AC2=C′C·BC,
∴AB2+AC2= B′B·BC+ C′C·BC=BC·(B′B+ C′C),即:AB2+AC2= BC·(B′B+ C′C);
故本題答案依次為:BC,BC,BC·(B′B+ C′C);
(2)由(1)可知AB2+AC2= BC·(B′B+ C′C),
∵AB=4,AC=3,BC=6,
∴16+9=6(B′B+ C′C),
∴B′B+ C′C=![]() ,
,
又∵B′B+ C′C=BC-B′C′,
∴B′C′=![]() .
.
即本題答案為: ![]() .
.


 陽光課堂課時優(yōu)化作業(yè)系列答案
陽光課堂課時優(yōu)化作業(yè)系列答案科目:初中數(shù)學 來源: 題型:
【題目】某學校計劃購買若干臺電腦,現(xiàn)從兩家商場了解到同一型號電腦每臺報價均為4000元,并且多買都有一定的優(yōu)惠.甲商場的優(yōu)惠條件是:第一臺按原價收費,其余每臺優(yōu)惠25%;乙商場的優(yōu)惠條件是:每臺優(yōu)惠20%.
(1)設該學校所買的電腦臺數(shù)是x臺,選擇甲商場時,所需費用為![]() 元,選擇乙商場時,所需費用為
元,選擇乙商場時,所需費用為![]() 元,請分別寫出
元,請分別寫出![]() ,
, ![]() 與x之間的關系式;
與x之間的關系式;
(2)該學校如何根據(jù)所買電腦的臺數(shù)選擇到哪間商場購買,所需費用較少?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,矩形ABCD中,AB=6,BC=4,過對角線BD中點O的直線分別交AB,CD邊于點E,F(xiàn).
(1)求證:四邊形BEDF是平行四邊形;
(2)當四邊形BEDF是菱形時,求EF的長.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】小莉的爸爸買了某演唱會的一張門票,她和哥哥兩人都想去觀看,可門票只有一張,讀九年級的哥哥想了一個辦法,拿了八張撲克牌,將數(shù)字 1,2,3,5 的四張牌給小莉,將數(shù)字為 4,6,7,8 的四張牌留給自己,并按如下游戲規(guī)則進行:小莉和哥哥從各自的四張牌中隨機抽出一張,然后 將抽出的兩張牌數(shù)字相加,如果和為偶數(shù),則小莉去,如果和為奇數(shù),則哥哥去。
(1)請用樹狀圖或列表的方法表示出兩張牌數(shù)字相加和的所有可能出現(xiàn)的結果;
(2)哥哥設計的游戲規(guī)則公平么?請說明理由。
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
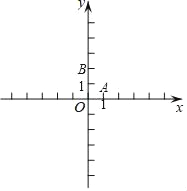
【題目】已知在平面直角坐標系xOy(如圖)中,已知拋物線y=![]() +bx+c點經過A(1,0)、B(0,2).
+bx+c點經過A(1,0)、B(0,2).
(1)求該拋物線的表達式;
(2)設該拋物線的對稱軸與x軸的交點為C,第四象限內的點D在該拋物線的對稱軸上,如果以點A、C、D所組成的三角形與△AOB相似,求點D的坐標;
(3)設點E在該拋物線的對稱軸上,它的縱坐標是1,聯(lián)結AE、BE,求sin∠ABE.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖在平面直角坐標系xOy中,函數(shù)y1=![]() (x>0)的圖象與一次函數(shù)y2=kx-k的圖象的交點為A(m,2).
(x>0)的圖象與一次函數(shù)y2=kx-k的圖象的交點為A(m,2).
(1)求一次函數(shù)的解析式;
(2)設一次函數(shù)y=kx-k的圖象與y軸交于點B,若點P是x軸上一點,且滿足△PAB的面積是6,請寫出點P的坐標.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
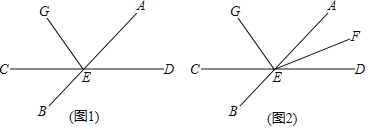
【題目】如圖,直線AB與CD相交于點E,射線EG在∠AEC內(如圖1).
(1)若∠BEC的補角是它的余角的3倍,則∠BEC= °;
(2)在(1)的條件下,若∠CEG比∠AEG小25度,求∠AEG的大小;
(3)若射線EF平分∠AED,∠FEG=m°(m>90°)(如圖2),則∠AEG﹣∠CEG= °(用m的代表式表示).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
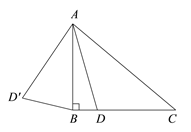
【題目】如圖,在△ABC中, ![]() ,
, ![]() °,點D是線段BC上的動點,將線段AD繞點A順時針旋轉50°至
°,點D是線段BC上的動點,將線段AD繞點A順時針旋轉50°至![]() ,連接
,連接![]() .已知AB
.已知AB![]() 2cm,設BD為x cm,B
2cm,設BD為x cm,B![]() 為y cm.
為y cm.
小明根據(jù)學習函數(shù)的經驗,對函數(shù)y隨自變量x的變化而變化的規(guī)律進行了探究,下面是小明的探究過程,請補充完整.(說明:解答中所填數(shù)值均保留一位小數(shù))
(1)通過取點、畫圖、測量,得到了![]() 與
與![]() 的幾組值,如下表:
的幾組值,如下表:
|
| 0.5 | 0.7 | 1.0 | 1.5 | 2.0 | 2.3 |
| 1.7 | 1.3 | 1.1 | 0.7 | 0.9 | 1.1 |
(2)建立平面直角坐標系,描出以補全后的表中各對對應值為坐標的點,畫出該函數(shù)的圖象.

(3)結合畫出的函數(shù)圖象,解決問題:
線段![]() 的長度的最小值約為__________
的長度的最小值約為__________ ![]() ;
;
若![]()
![]() ,則
,則![]() 的長度x的取值范圍是_____________.
的長度x的取值范圍是_____________.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在直角坐標系中,已知點A(﹣3,0)、B(0,4),對△OAB連續(xù)作翻轉變換,依次得到△1、△2、△3、△4…,則△23中的![]() 的坐標為_______________。
的坐標為_______________。

查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com