
【題目】如圖所示,一次函數(shù)y1=x+1的圖象與x軸交于點A,與反比例函數(shù)![]() 的圖象在第一象限內(nèi)交于點B,作BC⊥x軸,垂足為C,且OC=1.
的圖象在第一象限內(nèi)交于點B,作BC⊥x軸,垂足為C,且OC=1.
(1)請直接寫出在第一象限內(nèi),當(dāng)x取何值時,y1>y2?
(2)將線段BC沿一次函數(shù)的圖象平移至點B與點A重合,平移后點C的對應(yīng)點是否在反比例函數(shù)的圖象上?

【答案】(1)x>1;(2)在
【解析】(1)根據(jù)圖象可知,在點B的右側(cè),一次函數(shù)的圖象y1=x+1在反比例函數(shù)圖象![]() 的上方,且點B的橫坐標(biāo)為1,可知當(dāng)x>1時,y1>y2;(2)把x=1代入y1=x+1求出B點坐標(biāo)(1,2),用待定系數(shù)法求出反比例函數(shù)解析式,之后用一次函數(shù)求出A點坐標(biāo)(-1,0),根據(jù)BC的長是2,判斷點(-1,-2)是否在反比例函數(shù)圖象上即可得出結(jié)論.
的上方,且點B的橫坐標(biāo)為1,可知當(dāng)x>1時,y1>y2;(2)把x=1代入y1=x+1求出B點坐標(biāo)(1,2),用待定系數(shù)法求出反比例函數(shù)解析式,之后用一次函數(shù)求出A點坐標(biāo)(-1,0),根據(jù)BC的長是2,判斷點(-1,-2)是否在反比例函數(shù)圖象上即可得出結(jié)論.
解:(1)當(dāng)x>1時,y1>y2
(2)∵BC⊥x軸,垂足為C,且OC=1
∴C(1,0),點B的橫坐標(biāo)為1
當(dāng)x=1時,y1=x+1=2,∴B(1,2)
∵點B在反比例函數(shù)的圖象上
∴![]() ,∴k=2
,∴k=2
由y1=x+1=0,解得x=-1,∴A(-1,0)
∴將線段BC沿一次函數(shù)的圖象平移至點B與點A重合時,線段BC向下平移了2個單位,向左平移了2個單位,平移后點C的對應(yīng)點的坐標(biāo)為(-1,-2)
當(dāng)x=-1時, ![]()
∴平移后點C的對應(yīng)點在反比例函數(shù)的圖象上


 開心快樂假期作業(yè)暑假作業(yè)西安出版社系列答案
開心快樂假期作業(yè)暑假作業(yè)西安出版社系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,正方形ABCD中,CD=6,點E在邊CD上,且CD=3DE.將△ADE沿AE對折至△AFE,延長EF交邊BC于點G,連結(jié)AG、CF. 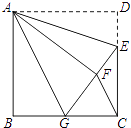
(1)求證:①△ABG≌△AFG; ②求GC的長;
(2)求△FGC的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知:如圖,把矩形OCBA放置于直角坐標(biāo)系中,OC=3,BC=2,取AB的中點M,連結(jié)MC,把△MBC沿x軸的負(fù)方向平移OC的長度后得到△DAO.

(1)直接寫出點D的坐標(biāo);
(2)已知點B與點D在經(jīng)過原點的拋物線上,點P在第一象限內(nèi)的該拋物線上移動,過點P作PQ⊥x軸于點Q,連結(jié)OP.
①若以O、P、Q為頂點的三角形與△DAO相似,試求出點P的坐標(biāo);
②試問在拋物線的對稱軸上是否存在一點T,使得![]() 的值最大.若存在,求出T點坐標(biāo);若不存在,請說明理由.
的值最大.若存在,求出T點坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某學(xué)校計劃購進(jìn)一批電腦和電子白板,經(jīng)過市場考察得知,購買1臺電腦和2臺電子白板需要3.5萬元,購買2臺電腦和1臺電子白板需要2.5萬元.
(1)求每臺電腦,每臺電子白板各多少萬元?
(2)根據(jù)學(xué)校實際,需至少購進(jìn)電腦和電子白板共30臺,總費用不超過28萬元,那么電子白板最多能買幾臺?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某牧場,放養(yǎng)的鴕鳥和奶牛一共70只,已知鴕鳥和奶牛的腿數(shù)之和為196條,則鴕鳥的頭數(shù)比奶牛多( )
A.20只
B.14只
C.15只
D.13只
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com