
【題目】如圖,在△ABC中,∠BAC=60°,BP平分∠ABC,CP平分∠ACB,求∠BPC的度數. 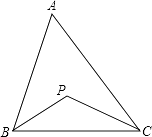
【答案】解:∵△ABC中,∠A=60°,
∴∠ABC+∠ACB=120°.
∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC+∠PCB= ![]() (∠ABC+∠ACB)=60°.
(∠ABC+∠ACB)=60°.
∵∠PBC+∠PCB+∠BPC=180°,
∴∠BPC=180°﹣60°=120°.
故答案為:120°
【解析】先根據三角形內角和定理求出∠ABC+∠ACB的度數,再由角平分線的性質得出∠PBC+∠PCB的度數,由三角形內角和定理即可得出結論.
【考點精析】通過靈活運用三角形的內角和外角,掌握三角形的三個內角中,只可能有一個內角是直角或鈍角;直角三角形的兩個銳角互余;三角形的一個外角等于和它不相鄰的兩個內角的和;三角形的一個外角大于任何一個和它不相鄰的內角即可以解答此題.


科目:初中數學 來源: 題型:
【題目】如圖,已知直線y=﹣x和反比例函數 ![]() (k>0),點A(m,n)(m>0)在反比例函數
(k>0),點A(m,n)(m>0)在反比例函數![]() 上.
上.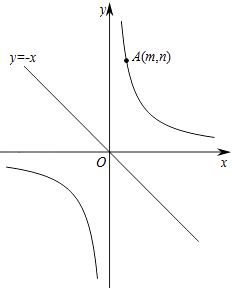
(1)當m=n=2時,
①直接寫出k的值;
②將直線y=﹣x作怎樣的平移能使平移后的直線與反比例函數 ![]() 只有一個交點.
只有一個交點.
(2)將直線y=﹣x繞著原點O旋轉,設旋轉后的直線與反比例函數 ![]() 交于點B(a,b)(a>0,b>0)和點C.設直線AB,AC分別與x軸交于D,E兩點,試問:
交于點B(a,b)(a>0,b>0)和點C.設直線AB,AC分別與x軸交于D,E兩點,試問: ![]() 與
與 ![]() 的值存在怎樣的數量關系?請說明理由.
的值存在怎樣的數量關系?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】給出下列算式:①(a3)2=a3×2=a6;②aman=am+n(m,n為正整數);③[(-x)4]5=-x20.其中正確的算式有( ).
A. 0個B. 1個C. 2個D. 3個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知m+a=n+b,根據等式性質變形為m=n,那么a,b必須符合的條件是( )
A.a=﹣b
B.﹣a=b
C.a=b
D.a,b可以是任意有理數或整式
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,點A的坐標為(﹣1,﹣2),將OA繞原點O逆時針旋轉180°得到OA′,點A′的坐標為(a,b),則a﹣b等于( )
A.1
B.﹣1
C.3
D.﹣3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com