
【題目】解下列方程:
(1)2x2+3=7x;
(2)(x+4)2=5(x+4);
(3)x2﹣5x+1=0(用配方法);
(4)2x2﹣2 ![]() x﹣5=0.
x﹣5=0.
【答案】
(1)解:2x2﹣7x+3=0,
∴(x﹣3)(2x﹣1)=0,
∴x﹣3=0或2x﹣1=0,
解得:x=3或x= ![]()
(2)解:∵(x+4)2﹣5(x+4)=0,
(x+4)(x﹣1)=0,
∴x+4=0或x﹣1=0,
解得:x=﹣4或x=1
(3)解:x2﹣5x=﹣1,
x2﹣5x+ ![]() =﹣1+
=﹣1+ ![]() ,
,
即(x﹣ ![]() )2=
)2= ![]() ,
,
∴x﹣ ![]() =±
=± ![]() ,
,
即x1= ![]() ,x2=
,x2= ![]()
(4)解:2x2﹣2 ![]() x﹣5=0,
x﹣5=0,
∵a=2,b=﹣2 ![]() ,c=﹣5,
,c=﹣5,
∴△=8+4×2×5=48>0,
∴x= ![]() =
= ![]()
【解析】(1)因式分解法求解可得;(2)提取公因式法求解可得;(3)配方法求解即可得;(4)公式法求解可得.
【考點精析】本題主要考查了配方法和因式分解法的相關知識點,需要掌握左未右已先分離,二系化“1”是其次.一系折半再平方,兩邊同加沒問題.左邊分解右合并,直接開方去解題;已知未知先分離,因式分解是其次.調整系數等互反,和差積套恒等式.完全平方等常數,間接配方顯優勢才能正確解答此題.


科目:初中數學 來源: 題型:
【題目】小明家(記為A)、他上學的學校(記為B)、書店(記為C)依次坐落在一條東西走向的大街上,小明家位于學校西邊250米處,書店位于學校東邊100米處,小明中午放學后,到書店買本輔導書,然后回家吃中午飯,下午直接去學校上課.
(1)試用數軸表示出小明家(A)、學校(B)、書店(C)的位置;
(2)計算出小明家與書店的距離;
(3)小明從中午放學離校到下午上學到校一共走了多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小梅在瀏覽某電影評價網站時,搜索了最近關注到的甲、乙、丙三部電影,網站通過對觀眾的抽樣調查,得到這三部電影的評分數據統計圖分別如下:
甲、乙、丙三部電影評分情況統計圖
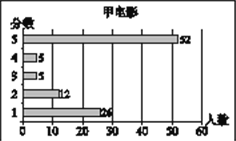


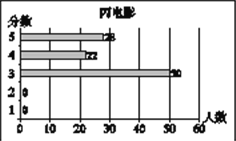
根據以上材料回答下列問題:
(1)小梅根據所學的統計知識,對以上統計圖中的數據進行了分析,并通過計算得到這三部電影抽樣調查的樣本容量,觀眾評分的平均數、眾數、中位數,請你將下表補充完整:
甲、乙、丙三部電影評分情況統計表
電影 | 樣本容量 | 平均數 | 眾數 | 中位數 |
甲 | 100 | 3.45 | 5 | |
乙 | 3.66 | 5 | ||
丙 | 100 | 3 | 3.5 |
(2)根據統計圖和統計表中的數據,可以推斷其中_______電影相對比較受歡迎,理由是
_______________________________________________________________________.(至少從兩個不同的角度說明你推斷的合理性)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,拋物線 ![]() 與
與 ![]() 軸交于A、B兩點(點A在點B的左側),點B的坐標為(3,0),與
軸交于A、B兩點(點A在點B的左側),點B的坐標為(3,0),與 ![]() 軸交于點C(0,-3),頂點為D。
軸交于點C(0,-3),頂點為D。
(1)求拋物線的解析式及頂點D的坐標。
(2)聯結AC,BC,求∠ACB的正切值。
(3)點P是x軸上一點,是否存在點P使得△PBD與△CAB相似,若存在,請求出點P的坐標;若不存在,請說明理由。
(4)M是拋物線上一點,點N在 ![]() 軸,是否存在點N,使得以點A,C,M,N為頂點的四邊形是平行四邊形?若存在,請直接寫出點N的坐標;若不存在,請說明理由。
軸,是否存在點N,使得以點A,C,M,N為頂點的四邊形是平行四邊形?若存在,請直接寫出點N的坐標;若不存在,請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一輛警車在高速公路的A處加滿油,以每小時60千米的速度勻速行駛.已知警車一次加滿油后,油箱內的余油量y(升)與行駛時間x(小時)的函數關系的圖象如圖所示的直線l上的一部分.
(1)求直線l的函數關系式;
(2)如果警車要回到A處,且要求警車中的余油量不能少于10升,那么警車可以行駛到離A處的最遠距離是多少?
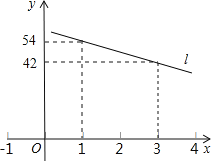
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△BAD是由△BEC在平面內繞點B旋轉60°而得,且AB⊥BC,BE=CE,連接DE. 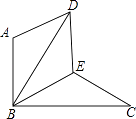
(1)求證:△BDE≌△BCE;
(2)試判斷四邊形ABED的形狀,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
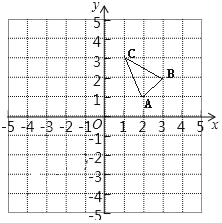
【題目】在邊長為1個單位長度的正方形網格中建立如圖所示的平面直角坐標系,△ABC的頂點都在格點上,請解答下列問題:
(1)作出△ABC向左平移4個單位長度后得到的△A1B1C1,并寫出點C1的坐標;
(2)將△A1B1C1繞原點O逆時針旋轉90°得到△A2B2C2,請畫出旋轉后的△A2B2C2,并寫出點C2的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,以O為圓心的弧 ![]() 度數為60°,∠BOE=45°,DA⊥OB,EB⊥OB.
度數為60°,∠BOE=45°,DA⊥OB,EB⊥OB. 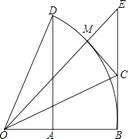
(1)求 ![]() 的值;
的值;
(2)若OE與 ![]() 交于點M,OC平分∠BOE,連接CM.說明CM為⊙O的切線;
交于點M,OC平分∠BOE,連接CM.說明CM為⊙O的切線;
(3)在(2)的條件下,若BC=1,求tan∠BCO的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com