
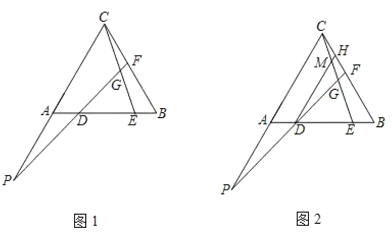
【題目】閱讀下列材料:數學課上,老師出示了這樣一個問題:
如圖1,在等邊![]() 中,點
中,點![]() 、
、![]() 在
在![]() 上,且
上,且![]() ,直線
,直線![]() 交
交![]() 于
于![]() 點,交
點,交![]() 延長線于
延長線于![]() 點,且
點,且![]() ,探究線段
,探究線段![]() 之間的數量關系,并證明.
之間的數量關系,并證明.
某學習小組的同學經過思考,交流了自己的想法:
小明:“通過觀察和度量,發現![]() 與
與![]() 存在某種數量關系”;
存在某種數量關系”;
小強:“通過觀察和度量,發現圖1中有一條線段與![]() 相等”;
相等”;
小偉:“通過構造三角形,證明三角形全等,進而可以得到線段![]() 之間的數量關系”.
之間的數量關系”.
……
老師:“保留原題條件,再過點![]() 作
作![]() 交
交![]() 于
于![]() 與
與![]() 相交于點
相交于點![]() (如圖2)如果給出
(如圖2)如果給出![]() 的值,那么可以求出
的值,那么可以求出![]() 的值”.
的值”.
請回答:
(1)在圖1中找出![]() 與
與![]() 數量關系,并證明;
數量關系,并證明;
(2)在圖1中找出與線段![]() 相等的線段,并證明;
相等的線段,并證明;
(3)探究線段![]() 之間的數量關系,并證明;
之間的數量關系,并證明;
(4)若![]() ,求
,求![]() 的值(用含
的值(用含![]() 的代數式表示).
的代數式表示).
【答案】(1)![]() ,理由見詳解;(2)
,理由見詳解;(2)![]() ,理由見詳解;(3)
,理由見詳解;(3)![]() ,理由見詳解;(4)
,理由見詳解;(4)![]()
【解析】
(1)先根據三角形內角和定理得:∠BDF+∠DEG=120°,由三角形外角的性質得:∠DEG=60°+∠BCE,代入可得結論;
(2)先判斷出△ACD≌△BCE(SAS),得出∠ACD=∠BCE,CD=CE,進而判斷出∠ACD=∠P,得CD=DP,即可得出結論;
(3)如圖2,作輔助線構建三角形全等,證明![]() ,得
,得![]() ,
,![]() ,設
,設![]() ,則
,則![]() ,
,![]() ,由勾股定理得:
,由勾股定理得:![]() ,列方程可得結論;
,列方程可得結論;
(4)如圖3,作輔助線,設![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,證明
,證明![]() ,由
,由![]() 得
得![]() ,
,![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,即
,即![]() ,計算
,計算![]() ,證明
,證明![]() ,可得結論.
,可得結論.
解:(1)如圖1,∠BCE+∠BDF=60°,
證明:∵∠DGE=60°,
∴∠BDF+∠DEG=180°﹣60°=120°,
∵△ABC是等邊三角形,
∴∠B=60°,
∵∠DEG=∠B+∠BCE,
∴∠BDF+60°+∠BCE=120°,
∴∠BCE+∠BDF=60°;
(2)DP=CE,
證明:如圖1,連接CD,

∵△ABC是等邊三角形,
∴∠BAC=∠B=60°,AC=BC,
∵AD=BE,
∴△ACD≌△BCE(SAS),
∴∠ACD=∠BCE,CD=CE,
∵∠CAB=∠P+∠ADP=∠P+∠BDF=60°,
由(1)知:∠BDF+∠BCE=60°,
∴∠P=∠BCE=∠ACD,
∴CD=DP,
∴CE=DP;
(3)結論:AD2+ADBD+BD2=CE2,
證明:如圖2,在邊AC上截取AH=AD,連接DH,過D作DM⊥AC于M,連接CD,
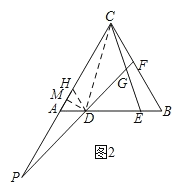
∴∠CAB=60°,
∴△ADH是等邊三角形,
∴AD=DH=AH,∠AHD=60°,
∴∠DHC=∠PAD=120°,
由(2)知CD=PD,∠P=∠ACD,
∴△DHC≌△DAP(AAS),
∴CH=AP,
∵AC=AB,AH=AD,
∴AC﹣AH=AB﹣AD,即CH=BD,
∴BD=AP,
Rt△ADM中,∠ADM=30°,
設![]() ,則
,則![]() ,
,![]() ,
,
![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,
,
![]()
![]() ,
,
![]() ;
;
(4)如圖3,連接CD,過H作HQ∥DF,交CD于Q,則∠QHD=∠MDG,

設CH=x,FH=y,FG=a,DG=na,CE=CD=ma,
∵DH∥AC,
∴∠DHF=∠ACB=60°,
∵∠CGF=∠DGE=60°,
∴∠DHF=∠CGF,
∵∠DFH=∠CFG,
∴∠MDG=∠MCH,△CGF∽△DHF,
∵DH∥AC,
∴∠CDH=∠ACD=∠GCF=∠MDG=∠QHD,
∴QH=QD,
∵QH∥DF,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,即
,即![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,即
,即![]() ,
,
![]()
 ,
,
![]() ,
,
∵∠MCH=∠MDG,∠CMH=∠DMG,
∴△CMH∽△DMG,
![]()
 .
.


科目:初中數學 來源: 題型:
【題目】如圖,在邊長為4的正方形ABCD中,動點E以每秒1個單位長度的速度從點A開始沿邊AB向點B運動,動點F以每秒2個單位長度的速度從點B開始沿邊BC向點C運動,動點E比動點F先出發1秒,其中一個動點到達終點時,另一個動點也隨之停止運動設點F的運動時間為t秒.
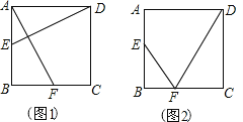
(1)如圖1,連接DE,AF.若DE⊥AF,求t的值;
(2)如圖2,連結EF,DF.當t為何值時,△EBF∽△DCF?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 與
與![]() 軸分別交于點
軸分別交于點![]() ,
,![]() ,與
,與![]() 軸交于點
軸交于點![]() ,頂點為
,頂點為![]() ,對稱軸交
,對稱軸交![]() 軸于點
軸于點![]() .
.
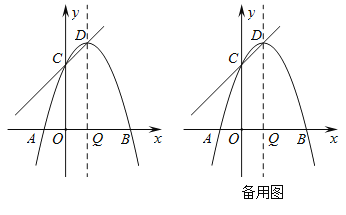
(1)求拋物線的解析式.
(2)若點![]() 是拋物線的對稱軸上的一點,以點
是拋物線的對稱軸上的一點,以點![]() 為圓心的圓經過
為圓心的圓經過![]() ,
,![]() 兩點,且與直線
兩點,且與直線![]() 相切,求點
相切,求點![]() 的坐標.
的坐標.
(3)在拋物線的對稱軸上是否存在一點![]() ,使得
,使得![]() 與
與![]() 相似?如果存在,求出點
相似?如果存在,求出點![]() 的坐標;如果不存在,請說明理由.
的坐標;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
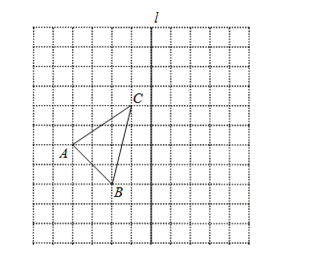
【題目】如圖,在![]() 的正方形網格中,每個小正方形的邊長都為1,網格中有一個格點
的正方形網格中,每個小正方形的邊長都為1,網格中有一個格點![]() (即三角形的頂點都在格點上).
(即三角形的頂點都在格點上).
(1)在圖中作出![]() 關于直線l對稱的
關于直線l對稱的![]() ;(要求A與
;(要求A與![]() ,B與
,B與![]() ,C與
,C與![]() 相對應)
相對應)
(2)作出![]() 繞點C順時針方向旋轉90°后得到的
繞點C順時針方向旋轉90°后得到的![]() ;
;
(3)在(2)的條件下求出線段CB在旋轉中所掃過的面積.(結果保留π)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2019年5月“亞洲文明對話大會”在北京成功舉辦,引起了世界人民的極大關注,某市一研究機構為了了解![]() 歲年齡段市民對本次大會的關注程度,隨機選取了100名年齡在該范圍內的市民進行了調查,并將收集到的數據制成了如下尚不完整的頻數分布表、頻數分布走訪圖和扇形統計圖:
歲年齡段市民對本次大會的關注程度,隨機選取了100名年齡在該范圍內的市民進行了調查,并將收集到的數據制成了如下尚不完整的頻數分布表、頻數分布走訪圖和扇形統計圖:
組別 | 年齡段 | 頻數(人數) |
第1組 |
| 5 |
第2組 |
|
|
第3組 |
| 35 |
第4組 |
| 20 |
第5組 |
| 15 |
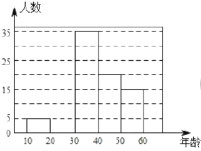
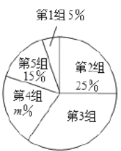
(1)請直接寫出![]() 、
、![]() 的值及扇形統計圖中第3組所對應的圓心角的度數;
的值及扇形統計圖中第3組所對應的圓心角的度數;
(2)請補全上面的頻數分布直方圖;
(3)假設該市現有![]() 歲的市民300萬人,問第4組年齡段關注本次大會的人數經銷商有多少萬人?
歲的市民300萬人,問第4組年齡段關注本次大會的人數經銷商有多少萬人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某區教育系統為了更好地宣傳掃黑除惡專項斗爭,印制了應知應會手冊,該區教育局想了解教師對掃黑除惡專項斗爭應知應會知識掌握程度,抽取了部分教師進行了測試,并將測試成績繪制成下面兩幅統計圖,請根據統計圖中提供的信息,回答下面問題:
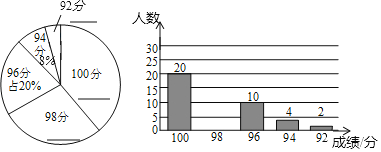
(1)計算樣本中,成績為98分的教師有 人,并補全兩個統計圖;
(2)樣本中,測試成績的眾數是 ,中位數是 ;
(3)若該區共有教師6880名,根據此次成績估計該區大約有多少名教師已全部掌握掃黑除惡專項斗爭應知應會知識?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在城市改造中,市政府欲在一條人工河上架一座橋,河的兩岸PQ與MN平行,河岸MN上有A、B兩個相距50米的涼亭,小亮在河對岸D處測得∠ADP=60°,然后沿河岸走了110米到達C處,測得∠BCP=30°,求這條河的寬.(結果保留根號)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2﹣2ax﹣2的圖象(記為拋物線C1)頂點為M,直線l:y=2x﹣a與x軸,y軸分別交于A,B.
(1)對于拋物線C1,以下結論正確的是 ;
①對稱軸是:直線x=1;②頂點坐標(1,﹣a﹣2);③拋物線一定經過兩個定點.
(2)當a>0時,設△ABM的面積為S,求S與a的函數關系;
(3)將二次函數y=ax2﹣2ax﹣2的圖象C1繞點P(t,﹣2)旋轉180°得到二次函數的圖象(記為拋物線C2),頂點為N.
①當﹣2≤x≤1時,旋轉前后的兩個二次函數y的值都會隨x的增大而減小,求t的取值范圍;
②當a=1時,點Q是拋物線C1上的一點,點Q在拋物線C2上的對應點為Q',試探究四邊形QMQ'N能否為正方形?若能,求出t的值,若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將Rt△ABC繞直角頂點B逆時針旋轉90°得到△DBE,DE的延長線恰好經過AC的中點F,連接AD,CE.
(1)求證:AE=CE;
(2)若BC=![]() ,求AB的長.
,求AB的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com