
【題目】某商場將進貨價為30元的臺燈以40元的價格售出,平均每月能售出600個,這種臺燈的售價每上漲1元,其銷量就減少10個,
(1)為了實現銷售這種臺燈平均每月10000元的銷售利潤,售價應定為多少元?
(2)當售價定為多少元時,其銷售利潤達到最大,最大利潤是多少?
【答案】(1)50或80; (2) 售價為65元時利潤最大,利潤最大為12250元;
【解析】
(1) 假設這種臺燈上漲x元,根據題意列出方程![]() ,再求解即可得到答案;
,再求解即可得到答案;
(2)根據利潤=每個臺燈的利潤×銷售量列出一元二次方程,再根據二次函數的性質求最大利潤即可得到答案;
解:(1) 假設這種臺燈上漲x元,根據題意可得方程:
![]() ,
,
即:![]() ,
,
化簡得:![]() ,
,
即:![]()
解得:![]() 或
或![]() ,
,
此時售價定價為:10+40=50(元)或者40+40=80(元);
(2)設臺燈售價為x元,利潤為y元,根據題意得:
![]() ,
,
即:![]() ,
,
化簡得:![]()
即:![]() ,
,
根據二次函數的性質,開口向下,越靠近對稱軸的點對應的值越大,對稱軸處取得最大值,
因此,當x=65時,取得最大利潤y=12250;
故售價為65元時利潤最大為12250元;


 考前必練系列答案
考前必練系列答案科目:初中數學 來源: 題型:
【題目】如圖,AD是等邊三角形ABC的高,點E是AD上的一個動點(點E不與點A重合),連接CE,將線段CE繞點E順時針旋轉60°得到EF,連接BF、CF.
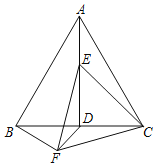
(1)猜想:△CEF是 三角形;
(2)求證:AE=BF;
(3)若AB=4,連接DF,在點E運動的過程中,請直接寫出DF的最小值 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點A(a﹣2b,2﹣4ab)在拋物線y=x2+4x+10上,則點A關于拋物線對稱軸的對稱點坐標為( )
A. (﹣3,7) B. (﹣1,7) C. (﹣4,10) D. (0,10)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】設函數![]() (
(![]() 為常數),下列說法正確的是( ).
為常數),下列說法正確的是( ).
A. 對任意實數![]() ,函數與
,函數與![]() 軸都沒有交點
軸都沒有交點
B. 存在實數![]() ,滿足當
,滿足當![]() 時,函數
時,函數![]() 的值都隨
的值都隨![]() 的增大而減小
的增大而減小
C. ![]() 取不同的值時,二次函數
取不同的值時,二次函數![]() 的頂點始終在同一條直線上
的頂點始終在同一條直線上
D. 對任意實數![]() ,拋物線
,拋物線![]() 都必定經過唯一定點
都必定經過唯一定點
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一座橋如圖,橋下水面寬度AB是20米,高CD是4米.要使高為3米的船通過,則其寬度須不超過多少米.
(1)如圖1,若把橋看做是拋物線的一部分,建立如圖坐標系.
①求拋物線的解析式;
②要使高為3米的船通過,則其寬度須不超過多少米?
(2)如圖2,若把橋看做是圓的一部分.
①求圓的半徑;
②要使高為3米的船通過,則其寬度須不超過多少米?

查看答案和解析>>
科目:初中數學 來源: 題型:
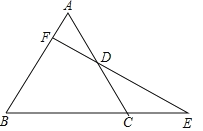
【題目】如圖,△ABC是等邊三角形,延長BC到E,使CE=![]() BC.點D是邊AC的中點,連接ED并延長ED交AB于F,求證:
BC.點D是邊AC的中點,連接ED并延長ED交AB于F,求證:
(1)EF⊥AB;(2)DE=2DF.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩個服裝廠加工同種型號的防護服,甲廠每天加工的數量是乙廠每天加工數量的1.5倍,兩廠各加工600套防護服,甲廠比乙廠要少用4天.
(1)求甲、乙兩廠每天各加工多少套防護服?
(2)已知甲、乙兩廠加工這種防護服每天的費用分別是150元和120元,疫情期間,某醫院緊急需要3000套這種防護服,甲廠單獨加工一段時間后另有安排,剩下任務只能由乙單獨完成.如果總加工費不超過6360元,那么甲廠至少要加工多少天?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com