
【題目】如圖,正方形ABCD中,AB=8cm,對角線AC,BD相交于點O,點E,F分別從B,C兩點同時出發,以1cm/s的速度沿BC,CD運動,到點C,D時停止運動,設運動時間為t(s),△OEF的面積為s(cm2),則s(cm2)與t(s)的函數關系可用圖象表示為( )
A.
B.
C.
D.
【答案】B
【解析】解:根據題意BE=CF=t,CE=8﹣t,
∵四邊形ABCD為正方形,
∴OB=OC,∠OBC=∠OCD=45°,
∵在△OBE和△OCF中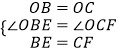 ,
,
∴△OBE≌△OCF(SAS),
∴S△OBE=S△OCF ,
∴S四邊形OECF=S△OBC= ![]() ×82=16,
×82=16,
∴S=S四邊形OECF﹣S△CEF=16﹣ ![]() (8﹣t)t=
(8﹣t)t= ![]() t2﹣4t+16=
t2﹣4t+16= ![]() (t﹣4)2+8(0≤t≤8),
(t﹣4)2+8(0≤t≤8),
∴s(cm2)與t(s)的函數圖象為拋物線一部分,頂點為(4,8),自變量為0≤t≤8.
故選:B.
由點E,F分別從B,C兩點同時出發,以1cm/s的速度沿BC,CD運動,得到BE=CF=t,則CE=8﹣t,再根據正方形的性質得OB=OC,∠OBC=∠OCD=45°,然后根據“SAS”可判斷△OBE≌△OCF,所以S△OBE=S△OCF , 這樣S四邊形OECF=S△OBC=16,于是S=S四邊形OECF﹣S△CEF=16﹣ ![]() (8﹣t)t,然后配方得到S=
(8﹣t)t,然后配方得到S= ![]() (t﹣4)2+8(0≤t≤8),最后利用解析式和二次函數的性質對各選項進行判斷.
(t﹣4)2+8(0≤t≤8),最后利用解析式和二次函數的性質對各選項進行判斷.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】把四張形狀大小完全相同的小長方形卡片(如圖①)不重疊的放在一個底面為長方形(長為m厘米,寬為n厘米)的盒子底部(如圖②),盒子底面未被卡片覆蓋的部分用陰影表示,則圖②中兩塊陰影部分的周長和是( )

A. 4m厘米 B. 4n厘米 C. 2(m+n)厘米 D. 4(m-n)厘米
查看答案和解析>>
科目:初中數學 來源: 題型:
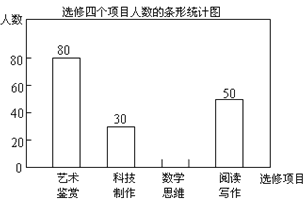
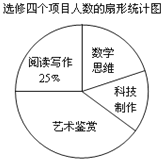
【題目】某校為了解“課程選修”的情況,對報名參加“藝術鑒賞”,“科技制作”,“數學思維”,“閱讀寫作”這四個選修項目的學生(每人限報一課)進行抽樣調查,下面是根據收集的數據繪制的不完整的統計圖:
請根據圖中提供的信息,解答下面的問題:
(1)此次共調查了___名學生,扇形統計圖中“藝術鑒賞”部分的圓心角是___度;
(2)此次調查“數學思維”的人數為_________,并補充完整條形圖;
(3)現該校共有600名學生報名參加這四個選修項目,請你估計其中有____名學生選修“科技制作”項目.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將正方體骰子(相對面上的點數分別為1和6、2和5、3和4)放置于水平桌面上,如圖1。在圖2中,將骰子向右翻滾90°,然后在桌面上按逆時針方向旋轉90°,則完成一次變換。若骰子的初始位置為圖1所示的狀態,那么按上述規則連續完成14次變換后,骰子朝上一面的點數是_____________________。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】近兩年,國際市場黃金價格漲幅較大,中國交通銀行推出“沃德金”的理財產品,即以黃金為投資產品,投資者從黃金價格的上漲中賺取利潤.上周五黃金的收盤價為![]() 元/克,下表是本周星期一至星期五黃金價格的變化情況.(注:星期一至星期五開市,星期六、星期日休市)
元/克,下表是本周星期一至星期五黃金價格的變化情況.(注:星期一至星期五開市,星期六、星期日休市)
星期 | 一 | 二 | 三 | 四 | 五 |
收盤價的變化(與前一天收盤價比較) |
|
|
|
|
|
問
![]() 本周星期三黃金的收盤價是多少?
本周星期三黃金的收盤價是多少?
![]() 本周黃金收盤時的最高價、最低價分別是多少?
本周黃金收盤時的最高價、最低價分別是多少?
![]() 上周,小王以周五的收盤價
上周,小王以周五的收盤價![]() 元/克買入黃金
元/克買入黃金![]() 克,已知買入與賣出時均需支付成交金額的千分之五的交易費,賣出黃金時需支付成交金額的千分之三的印花稅.本周,小王以周五的收盤價全部賣出黃金
克,已知買入與賣出時均需支付成交金額的千分之五的交易費,賣出黃金時需支付成交金額的千分之三的印花稅.本周,小王以周五的收盤價全部賣出黃金![]() 克,他的收益情況如何?
克,他的收益情況如何?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,D是AB上一點,DF交AC于點E,FC∥AB,則下列結論錯誤的是( )

A. 若AE=CE,則DE=FE B. 若DE=FE,則AE=CE
C. 若BC=CF,則AD=CF D. 若AD=CF,則DE=FE
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料,解答問題.
飲水問題是關系到學生身心健康的重要生活環節,東坡中學共有教學班24個,平均每班有學生50人,經估算,學生一年在校時間約為240天(除去各種節假日),春、夏、秋、冬季各60天.原來,學生飲水一般都是購純凈水(其他碳酸飲料或果汁價格更高),純凈水零售價為1.5元/瓶,每個學生春、秋、冬季平均每天買1瓶純凈水,夏季平均每天要買2瓶純凈水,學校為了減輕學生消費負擔,要求每個班自行購買1臺冷熱飲水機,經調查,購買一臺功率為500 W的冷熱飲水機約為150元,純凈水每桶6元,每班春、秋兩季,平均每1.5天購買4桶,夏季平均每天購買5桶,冬季平均每天購買1桶,飲水機每天開10小時,當地民用電價為0.50元/度.
問題:
(1)在未購買飲水機之前,全年平均每個學生要花費多少錢來購買純凈水飲用?
(2)在購買飲水機解決學生飲水問題后,每班當年共要花費多少元?
(3)這項便利學生的措施實施后,東坡中學當年全體學生共節約多少錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】88層的金茂大廈的電梯上,有顯示樓層的液晶屏,如圖,可顯示01,02,…,88,由于屏幕受到損壞,顯示左邊數字的7根線段中有1根不能亮了,顯示右邊數字的7根線段中有3根不能亮了。請問:電梯在運行的過程中,最多還有 _____個樓層的數字顯示是正確的.

(說明)數字0、1、2、3、4、5、6、7、8、9顯示方式如下圖所示.

![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列結論:w
①若a+b+c=0,且abc≠0,則方程a+bx+c=0的解是x=1;
②若a(x﹣1)=b(x﹣1)有唯一的解,則a≠b;
③若b=2a,則關于x的方程ax+b=0(a≠0)的解為x=﹣![]() ;
;
④若a+b+c=1,且a≠0,則x=1一定是方程ax+b+c=1的解;
其中結論正確個數有( )
A.4個 B.3個 C.2個 D.1個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com