
【題目】如圖,過(guò)∠AOB平分線(xiàn)上一點(diǎn)C作CD∥OB交OA于點(diǎn)D,E是線(xiàn)段OC的中點(diǎn),請(qǐng)過(guò)點(diǎn)E畫(huà)直線(xiàn)分別交射線(xiàn)CD、OB于點(diǎn)M、N,探究線(xiàn)段OD、ON、DM之間的數(shù)量關(guān)系,并證明你的結(jié)論.
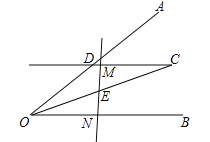
【答案】①當(dāng)M在線(xiàn)段CD上時(shí),OD=DM+ON;②當(dāng)M在線(xiàn)段CD延長(zhǎng)線(xiàn)上時(shí),OD=ON-DM,證明見(jiàn)試題解析.
【解析】
試題分析:分兩種情況討論,①當(dāng)M在線(xiàn)段CD上時(shí),由OC是∠AOB的平分線(xiàn),CD∥OB,得出∠DOC=∠DC0,故有OD=CD=DM+CM;再由E是線(xiàn)段OC的中點(diǎn),CD∥OB,得到CM=ON,即可得出OD=DM+ON;
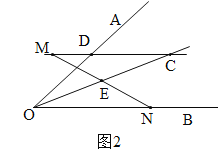
②當(dāng)M在線(xiàn)段CD延長(zhǎng)線(xiàn)上時(shí),OD=ON-DM,如圖2,同①可得OD=DC=CM-DM=ON-DM.
試題解析:①當(dāng)M在線(xiàn)段CD上時(shí),OD=DM+ON.證明如下:
∵OC是∠AOB的平分線(xiàn),∴∠DOC=∠C0B,又∵CD∥OB,∴∠DCO=∠C0B,∴∠DOC=∠DC0,∴OD=CD=DM+CM,∵E是線(xiàn)段OC的中點(diǎn),∴CE=OE,∵CD∥OB,∴![]() ,∴CM=ON,又∵OD=DM+CM,∴OD=DM+ON;
,∴CM=ON,又∵OD=DM+CM,∴OD=DM+ON;
②當(dāng)M在線(xiàn)段CD延長(zhǎng)線(xiàn)上時(shí),OD=ON-DM,如圖2,同①可得OD=DC=CM-DM=ON-DM.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知直線(xiàn)l上有一點(diǎn)O,點(diǎn)A、B同時(shí)從O出發(fā),在直線(xiàn)l上分別向左、向右作勻速運(yùn)動(dòng),且A、B的速度比為1:2,設(shè)運(yùn)動(dòng)時(shí)間為ts.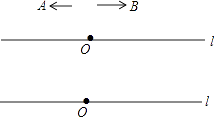
(1)當(dāng)t=2s時(shí),AB=12cm.此時(shí),
①在直線(xiàn)l上畫(huà)出A、B兩點(diǎn)運(yùn)動(dòng)2秒時(shí)的位置,并回答點(diǎn)A運(yùn)動(dòng)的速度是cm/s; 點(diǎn)B運(yùn)動(dòng)的速度是cm/s.
②若點(diǎn)P為直線(xiàn)l上一點(diǎn),且PA﹣PB=OP,求 ![]() 的值;
的值;
(2)在(1)的條件下,若A、B同時(shí)按原速向左運(yùn)動(dòng),再經(jīng)過(guò)幾秒,OA=2OB.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
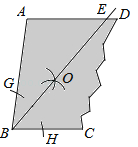
【題目】如圖,一塊余料ABCD,AD∥BC,現(xiàn)進(jìn)行如下操作:以點(diǎn)B為圓心,適當(dāng)長(zhǎng)為半徑畫(huà)弧,分別交BA,BC于點(diǎn)G,H;再分別以點(diǎn)G,H為圓心,大于![]() GH的長(zhǎng)為半徑畫(huà)弧,兩弧在∠ABC內(nèi)部相交于點(diǎn)O,畫(huà)射線(xiàn)BO,交AD于點(diǎn)E.
GH的長(zhǎng)為半徑畫(huà)弧,兩弧在∠ABC內(nèi)部相交于點(diǎn)O,畫(huà)射線(xiàn)BO,交AD于點(diǎn)E.
(1)求證:AB=AE;
(2)若∠A=100°,求∠EBC的度數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知:點(diǎn)A、C、B不在同一條直線(xiàn)上,AD∥BE
(1)如圖①,當(dāng)∠A=58°,∠B=118°時(shí),求∠C的度數(shù);
(2)如圖②,AQ、BQ分別為∠DAC、∠EBC的平分線(xiàn)所在直線(xiàn),試探究∠C與∠AQB的數(shù)量關(guān)系;
(3)如圖③,在(2)的前提下,且有AC∥QB,QP⊥PB,直接寫(xiě)出∠DAC:∠ACB:∠CBE的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某中學(xué)初一(二)班5位教師決定帶領(lǐng)本班a名學(xué)生在五一期間在元旦期間去珠海長(zhǎng)隆海洋王國(guó)旅游,每張票的價(jià)格為350元,A旅行社的收費(fèi)標(biāo)準(zhǔn)為:教師全價(jià),學(xué)生半價(jià);而B(niǎo)旅行社的收費(fèi)標(biāo)準(zhǔn)為:不分教師、學(xué)生,一律六折優(yōu)惠.
(1)分別用代數(shù)式表示參加這兩家旅行社所需的費(fèi)用;
A旅行社所需費(fèi)用為 元,B旅行社所需費(fèi)用為 元,
(2)如果這5位教師要帶領(lǐng)該班30名學(xué)生參加旅游,你認(rèn)為選擇哪一家旅行社較為合算,為什么?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】若順次連接四邊形ABCD各邊的中點(diǎn)所得四邊形是矩形,則四邊形ABCD一定滿(mǎn)足( )
A.對(duì)角線(xiàn)相等
B.對(duì)角線(xiàn)互相平分
C.對(duì)角線(xiàn)互相垂直
D.對(duì)角線(xiàn)相等且相互平分
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com