【題目】如圖，四邊形 ABCD 是矩形，把矩形沿直線 BD 拆疊，點 C 落在點 E 處，連接 DE， DE 與 AD 交于點 M．
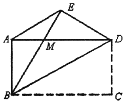
（1）證明四邊形 ABDE 是等腰梯形；
（2）寫出等腰梯形 ABDE 與矩形 ABCD 的面積大小關系，并證明你的結論．
【答案】（1）答案見解析；（2）等腰梯形ABDE小于矩形ABCD的面積
【解析】
（1）結合圖形證△AMB≌△EMD，再結合圖形的折疊關系可得答案．
（2） 由AE<BD,以及平行線間的距離相等，可得
由于
以及
可得結論.
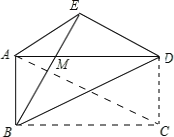
證明：(1)∵四邊形ABCD是矩形，
∴AD=BE,AB=ED,AD∥BC.
∴△ADB≌△DBC≌△EDB,∠EBD=∠DBC,∠ADB=∠EBD.
∴DM=BM，AM=EM.
∴△AMB≌△EMD.
∴AB=DE.AM=EM，
∴∠EAM=∠AEM，
∵DM=BM，
∴∠BDM=∠MBD，
又∵∠AME=∠BMD，
∴∠EAD=∠MDB，
∴AE∥BD.
∵AE≠BD，
∴四邊形ABDE是等腰梯形.
(2)∵
∵
∵AE<BD，
∴
∴
∴ 等腰梯形ABDE小于矩形ABCD的面積.
科目：初中數學 來源： 題型：
【題目】如圖，在矩形ABCD中，已知AB=2，BC=1.5，矩形在直線上繞其右下角的頂點B向右第一次旋轉90°至圖①位置，再繞右下角的頂點繼續向右第二次旋轉90°至圖②位置，…，以此類推，這樣連續旋轉2017次后，頂點A在整個旋轉過程中所經過的路程之和是_______.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】完成一項工作，如果安排兩個人合做，要
天才能完成.開始先安排一些人做
天后，又增加
人和他們一起做
天，結果完成了這項工作的一半，假設這些人的工作效率相同．
（1）開始安排了多少名工人?
（2）如果要求再用天做完剩余的全部工作，還需要再增加幾人一起做?
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】觀察下列等式：
第1個等式：a1＝
，
第2個等式：a2＝
，
第3個等式：a3＝
，
…
請解答下列問題：
(1)按以上規律列出第5個等式：a5＝ ＝ ；
(2)用含有n的代數式表示第n個等式：an＝ ＝ (n為正整數)；
(3)求a1+a2+a3+…+a2019的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點A的坐標為（0，1），點B是x軸正半軸上的一動點，以AB為邊作等腰Rt△ABC，使∠BAC=90°，設點B的橫坐標為x，設點C的縱坐標為y，能表示y與x的函數關系的圖象大致是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
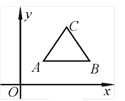
【題目】如圖，等邊三角形ABC的頂點A、B坐標分別為（1，1）、（3，1），若把等邊△ABC先沿x軸翻折，再向左平移1個單位”為第一次変換，則這樣連續經過2017次變換后，等邊△ABC的頂點C的坐標為_________.
查看答案和解析>>
科目：初中數學 來源： 題型：
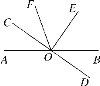
【題目】如圖，直線AB和CD交于點O，∠COE＝90°，OC平分∠AOF，∠COF＝35°.
（1）求∠BOD的度數；
（2）OE平分∠BOF嗎？請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
