
【題目】解答
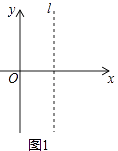
(1)觀察與歸納:在如圖1所示的平面直角坐標系中,直線l與y軸平行,點A與點B是直線l上的兩點(點A在點B的上方).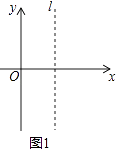
①小明發現:若點A坐標為(2,3),點B坐標為(2,﹣4),則AB的長度為;
②小明經過多次取l上的兩點后,他歸納出這樣的結論:若點A坐標為(t,m),點B坐標為(t,n),當m>n時,AB的長度可表示為;
(2)如圖2,正比例函數y=x與一次函數y=﹣x+6交于點A,點B是y=﹣x+6圖象與x軸的交點,點C在第四象限,且OC=5.點P是線段OB上的一個動點(點P不與點O,B重合),過點P與y軸平行的直線l交線段AB于點Q,交射線OC于R,設點P橫坐標為t,線段QR的長度為m.已知當t=4時,直線l恰好經過點C.
①求點A的坐標;
②求OC所在直線的關系式;
③求m關于t的函數關系式.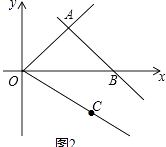
【答案】
(1)7;m﹣n
(2)
解:①解 ![]() 得
得 ![]() ,
,
∴A(3,3);
②∵直線l平行于y軸且當t=4時,直線l恰好過點C,如圖2,作CE⊥OB于E,
∴OE=4,
在Rt△OCE中,OC=5,
由勾股定理得:
CE= ![]() =3,
=3,
∴點C的坐標為:(4,﹣3);
設OC所在直線的關系式為y=kx,則﹣3=4k,
∴k=﹣ ![]() ,
,
∴OC所在直線的關系式為y=﹣ ![]() x;
x;
③由直線y=﹣x+6可知B(6,0),
作AD⊥OB于D,
∵A(3,3),
∴OD=BD=AD=3,
∴∠AOB=45°,OA=AB,
∴∠OAB=90°,∠ABO=45°
當0<t≤3時,如圖2,
∵直線l平行于y軸,
∴∠OPQ=90°,
∴∠OQP=45°,
∴OP=QP,
∵點P的橫坐標為t,
∴OP=QP=t,
在Rt△OCE中,
∵tan∠EOC=|k|= ![]() ,
,
∴tan∠POR= ![]() =
= ![]() ,
,
∴PR=OPtan∠POR= ![]() t,
t,
∴QR=QP+PR=t+ ![]() t=
t= ![]() t,
t,
∴m關于t的函數關系式為:m= ![]() t;
t;
當3<t<6時,如圖3,
∵∠BPQ=90°,∠ABO=45°,
∴∠BQP=∠PBQ=45°,
∴BP=QP,
∵點P的橫坐標為t,
∴PB=QP=6﹣t,
∵PR∥CE,
∴△BPR∽△BEC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得:PR=9﹣ ![]() t,
t,
∴QR=QP+PR=6﹣t+9﹣ ![]() t=15﹣
t=15﹣ ![]() t,
t,
∴m關于t的函數關系式為:m=15﹣ ![]() t;
t;
綜上,m關于t的函數關系式為m= 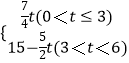
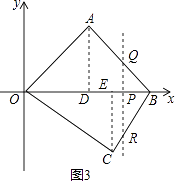

【解析】解:(1)①若點A坐標為(2,3),點B坐標為(2,﹣4),則AB的長度為3﹣(﹣4)=7;②若點A坐標為(t,m),點B坐標為(t,n),當m>n時,AB的長度可表示為m﹣n;
所以答案是7;m﹣n;
【考點精析】通過靈活運用正比例函數的圖象和性質和一次函數的圖象和性質,掌握正比函數圖直線,經過一定過原點.K正一三負二四,變化趨勢記心間.K正左低右邊高,同大同小向爬山.K負左高右邊低,一大另小下山巒;一次函數是直線,圖像經過仨象限;正比例函數更簡單,經過原點一直線;兩個系數k與b,作用之大莫小看,k是斜率定夾角,b與Y軸來相見,k為正來右上斜,x增減y增減;k為負來左下展,變化規律正相反;k的絕對值越大,線離橫軸就越遠即可以解答此題.


 字詞句段篇系列答案
字詞句段篇系列答案科目:初中數學 來源: 題型:
【題目】某小區為了綠化環境,計劃分兩次購進A、B兩種花草,第一次分別購進A、B兩種花草30棵和15棵,共花費675元;第二次分別購進A、B兩種花草12棵和5棵.兩次共花費940元(兩次購進的A、B兩種花草價格均分別相同).
(1)A、B兩種花草每棵的價格分別是多少元?
(2)若購買A、B兩種花草共31棵,且B種花草的數量少于A種花草的數量的2倍,請你給出一種費用最省的方案,并求出該方案所需費用.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著人們“節能環保,綠色出行”意識的增強,越來越多的人喜歡騎自行車出行,也給自行車商家帶來商機.某自行車行經營的A型自行車去年銷售總額為8萬元.今年該型自行車每輛售價預計比去年降低200元.若該型車的銷售數量與去年相同,那么今年的銷售總額將比去年減少10%,求:
(1)A型自行車去年每輛售價多少元?
(2)該車行今年計劃新進一批A型車和新款B型車共60輛,且B型車的進貨數量不超過A型車數量的兩倍.已知,A型車和B型車的進貨價格分別為1500元和1800元,計劃B型車銷售價格為2400元,應如何組織進貨才能使這批自行車銷售獲利最多?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某家具商場計劃購進某種餐桌、餐椅進行銷售,有關信息如表:

已知用600元購進的餐桌數量與用160元購進的餐椅數量相同.
(1)求表中a的值;
(2)若該商場購進餐椅的數量是餐桌數量的5倍還多20張,且餐桌和餐椅的總數量不超過200張.該商場計劃將一半的餐桌成套(一張餐桌和四張餐椅配成一套)銷售,其余餐桌、餐椅以零售方式銷售.請問怎樣進貨,才能獲得最大利潤?最大利潤是多少?
(3)由于原材料價格上漲,每張餐桌和餐椅的進價都上漲了10元,按照(2)中獲得最大利潤的方案購進餐桌和餐椅,在調整成套銷售量而不改變銷售價格的情況下,實際全部售出后,所得利潤比(2)中的最大利潤少了2250元.請問本次成套的銷售量為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】據有關部門統計,2019年春節期間,廣東各大景點的游客總數約25200000人次,將數25200000用科學記數法表示為( )
A.2.52×107B.2.52×108C.0.252×107D.0.252×108
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,分別以點A和點B為圓心,大于 ![]() AB的長為半徑畫弧,兩弧相交于點M,N,作直線MN,交BC于點D,連接AD.若△ADC的周長為10,AB=7,則△ABC的周長為 .
AB的長為半徑畫弧,兩弧相交于點M,N,作直線MN,交BC于點D,連接AD.若△ADC的周長為10,AB=7,則△ABC的周長為 . 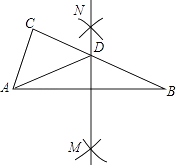
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com