
【題目】如圖, ![]() 是⊙O的直徑,點
是⊙O的直徑,點![]() 是
是![]() 的中點,連接
的中點,連接![]() 并延長至點
并延長至點![]() ,使
,使![]() ,點
,點![]() 是
是![]() 上一點,且
上一點,且![]() ,
, ![]() 的延長線交
的延長線交![]() 的延長線于點
的延長線于點![]() ,
, ![]() 交⊙O于點
交⊙O于點![]() ,連接
,連接![]() .
.
(1)求證: ![]() 是⊙O的切線;
是⊙O的切線;
(2)當![]() 時,求
時,求![]() 的長.
的長.

【答案】(1)證明見解析;(2)BH =![]() .
.
【解析】試題分析:(1)連接OC,由題意可得∠AOC=90°,OC//BD,從而得OB與BD垂直,問題得證;
(2)先證明△OCE∽△BFE,根據相似三角形對應邊成比例以及![]() ,求得BF=3,在Rt
,求得BF=3,在Rt![]() 中,利用勾股定理求得
中,利用勾股定理求得![]() ,再利用
,再利用![]() 即可得.
即可得.
試題解析:(1)連接OC,

∵AB為⊙O的直徑,點![]() 是
是![]() 的中點,∴∠AOC=90°,
的中點,∴∠AOC=90°,
∵![]() ,∴OC是
,∴OC是![]() 的中位線,∴OC∥BD,
的中位線,∴OC∥BD,
∴∠ABD=∠AOC=90°,
∴![]() ,
,
∴![]() 是⊙O的切線;
是⊙O的切線;
(2)由(1)知OC∥BD,∴△OCE∽△BFE,∴ ![]() ,
,
∵OB = 2,∴OC= OB = 2,AB = 4,∵ ![]() ,∴
,∴![]() ,∴BF=3,
,∴BF=3,
在Rt![]() 中,∠ABF=90°,
中,∠ABF=90°,![]() ,
,
∵![]() ,
,
∴![]() .即
.即![]() ,
,
∴BH =![]() .
.


 應用題天天練四川大學出版社系列答案
應用題天天練四川大學出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,直角坐標系中的網格由單位正方形構成,△ABC中,A點坐標為(2,3),B點坐標為(﹣2,0),C點坐標為(0,﹣1).
(1)S△ABC= ;
(2)若以A、B、C及點D為頂點的四邊形為平行四邊形,試在圖中畫出所有D點的位置并求出這些平行四邊形中最長的對角線長為 ,最短的對角線長為 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠CAB的平分線AD與BC的垂直平分線DE交于點D,DM⊥AB于M,DN⊥AC的延長線于N.
(1)求證:BM=CN;
(2)若AB=8,AC=4,求BM的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著中國傳統節日“端午節”的臨近,東方紅商場決定開展“歡度端午,回饋顧客”的讓利促銷活動,對部分品牌粽子進行打折銷售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,買6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,買50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙兩種品牌粽子每盒分別為多少元?
(2)陽光敬老院需購買甲品牌粽子80盒,乙品牌粽子100盒,問打折后購買這批粽子比不打折節省了多少錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y = x2 - 4x + 3.
(1)用配方法將y = x2 - 4x + 3化成y = a(x - h)2 + k的形式;
(2)在平面直角坐標系![]() 中畫出該函數的圖象;
中畫出該函數的圖象;
(3)當0≤x≤3時,y的取值范圍是 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】求不等式(2x﹣1)(x+3)>0的解集.
解:根據“同號兩數相乘,積為正”可得:①![]() 或 ②
或 ②![]() .
.
解①得x>![]() ;解②得x<﹣3.
;解②得x<﹣3.
∴不等式的解集為x>![]() 或x<﹣3.
或x<﹣3.
請你仿照上述方法解決下列問題:
(1)求不等式(2x﹣3)(x+1)<0的解集.
(2)求不等式![]() ≥0的解集.
≥0的解集.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小巖打算購買氣球裝扮學校“畢業典禮”活動會場,氣球的種類有笑臉和愛心兩種,兩種氣球的價格不同,但同一種氣球的價格相同.由于會場布置需要,購買時以一束(4個氣球)為單位,已知第一、二束氣球的價格如圖所示,則第三束氣球的價格為______元.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面材料:
在數學課上,老師提出如下問題:
尺規作圖:作已知角的角平分線.
已知:如圖,已知![]() .
.
求作: ![]() 的角平分線
的角平分線![]() .
.

小霞的作法如下:
(1)如圖,在平面內任取一點![]() ;
;
(2)以點![]() 為圓心,
為圓心, ![]() 為半徑作圓,交射線
為半徑作圓,交射線![]() 于點
于點![]() ,交射線
,交射線![]() 于點
于點![]() ;
;
(3)連接![]() ,過點
,過點![]() 作射線
作射線![]() 垂直線段
垂直線段![]() ,交⊙
,交⊙![]() 于點
于點![]() ;
;
(4)連接![]() .
.

所以射線![]() 為所求.
為所求.
老師說:“小霞的作法正確.”
請回答:小霞的作圖依據是___________________________________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
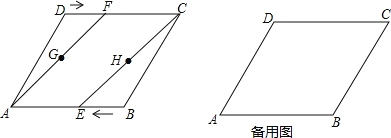
【題目】如圖,在菱形![]() ,
,![]() ,
,![]() .動點
.動點![]() 、
、![]() 分別從點
分別從點![]() 、
、![]() 同時出發,以
同時出發,以![]() 的速度向點
的速度向點![]() 、
、![]() 運動,連接
運動,連接![]() 、
、![]() ,取
,取![]() 、
、![]() 的中點
的中點![]() 、
、![]() ,連接
,連接![]() 、
、![]() .設運動的時間為
.設運動的時間為![]() .
.
(1)求證:![]() ;
;
(2)當![]() 為何值時,四邊形
為何值時,四邊形![]() 為菱形;
為菱形;
(3)試探究:是否存在某個時刻![]() ,使四邊形
,使四邊形![]() 為矩形,若存在,求出
為矩形,若存在,求出![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com