
【題目】在平面直角坐標系中,A(a,0),C(0,c)且滿足:(a+6)2+![]() =0,長方形ABCO在坐標系中(如圖),點O為坐標系的原點.
=0,長方形ABCO在坐標系中(如圖),點O為坐標系的原點.
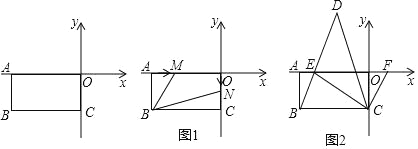
(1)求點B的坐標.
(2)如圖1,若點M從點A出發,以2個單位/秒的速度向右運動(不超過點O),點N從原點O出發,以1個單位/秒的速度向下運動(不超過點C),設M、N兩點同時出發,在它們運動的過程中,四邊形MBNO的面積是否發生變化?若不變,求其值;若變化,求變化的范圍.
(3)如圖2,E為x軸負半軸上一點,且∠CBE=∠CEB,F是x軸正半軸上一動點,∠ECF的平分線CD交BE的延長線于點D,在點F運動的過程中,請探究∠CFE與∠D的數量關系,并說明理由
【答案】(1)B(﹣6,﹣3);(2)四邊形MBNO的面積不變;是定值9;(3)∠CFE=2∠D.
【解析】
(1)根據題意可得a=﹣6,c=﹣3,則可求A點,C點,B點坐標;(2)設M、N同時出發的時間為t,則S四邊形MBNO=S長方形OABC﹣S△ABM﹣S△BCN=18﹣![]() ×2t×3﹣
×2t×3﹣![]() ×6×(3﹣t)=9.與時間無關.即面積是定值,其值為9;(3)根據三角形內角和定理和三角形外角等于不相鄰的兩個內角的和,可求∠CFE與∠D的數量關系.
×6×(3﹣t)=9.與時間無關.即面積是定值,其值為9;(3)根據三角形內角和定理和三角形外角等于不相鄰的兩個內角的和,可求∠CFE與∠D的數量關系.
解:(1)∵(a+6)2+![]() =0,
=0,
∴a=﹣6,c=﹣3
∴A(﹣6,0),C(0,﹣3)
∵四邊形OABC是矩形
∴AO∥BC,AB∥OC,AB=OC=3,AO=BC=6
∴B(﹣6,﹣3)
(2)四邊形MBNO的面積不變.
設M、N同時出發的時間為t,
則S四邊形MBNO=S長方形OABC﹣S△ABM﹣S△BCN=18﹣![]() ×2t×3﹣
×2t×3﹣![]() ×6×(3﹣t)=9.與時間無關.
×6×(3﹣t)=9.與時間無關.
∴在運動過程中面積不變.是定值9
(3)∠CFE=2∠D.
理由如下:如圖
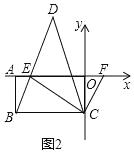
∵∠CBE=∠CEB
∴∠ECB=180°﹣2∠BEC
∵CD平分∠ECF
∴∠DCE=∠DCF
∵AF∥BC
∴∠F=180°﹣∠DCF﹣∠DCE﹣∠BCE=180°﹣2∠DCE﹣(180°﹣2∠BEC)
∴∠F=2∠BEC﹣2∠DCE
∵∠BEC=∠D+∠DCE
∴∠F=2(∠D+∠DCE)﹣2∠DCE
∴∠F=2∠D


科目:初中數學 來源: 題型:
【題目】新園小區計劃在一塊長為20米,寬12米的矩形場地上修建三條互相垂直的長方形甬路(一條橫向、兩條縱向,且橫向、縱向的寬度比為3:2),其余部分種花草.若要使種花草的面積達到144米2.則橫向的甬路寬為_____米.

查看答案和解析>>
科目:初中數學 來源: 題型:
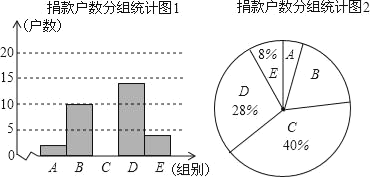
【題目】為了讓更多的失學兒童重返校園,某社區組織“獻愛心手拉手”捐款活動.對社區部分捐款戶數進行調查和分組統計后,將數據整理成如圖所示的統計圖和統計表(圖中信息不完整).已知A、B兩組捐款戶數的比為1:5.請結合以上信息解答下列問題.捐款戶數分組統計表
組別 | 捐款額(x)元 | 戶數 |
A | 1≤x<50 | a |
B | 50≤x<100 | 10 |
C | 100≤x<150 |
|
D | 150≤x<200 |
|
E | x≥200 |
|
(1)a= ,本次調查樣本的容量是 ;
(2)補全“捐款戶數分組統計圖1和捐款戶數分組統計表”;
(3)若該社區有2000戶住戶,請根據以上信息,估計全社區捐款不少于150元的戶數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校研究性學習小組在學習二次根式 ![]() =|a|之后,研究了如下四個問題,其中錯誤的是( )
=|a|之后,研究了如下四個問題,其中錯誤的是( )
A.在a>1的條件下化簡代數式a+ ![]() 的結果為2a﹣1
的結果為2a﹣1
B.當a+ ![]() 的值恒為定值時,字母a的取值范圍是a≤1
的值恒為定值時,字母a的取值范圍是a≤1
C.a+ ![]() 的值隨a變化而變化,當a取某個數值時,上述代數式的值可以為
的值隨a變化而變化,當a取某個數值時,上述代數式的值可以為 ![]()
D.若 ![]() =(
=( ![]() )2 , 則字母a必須滿足a≥1
)2 , 則字母a必須滿足a≥1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀與計算:請閱讀以下材料,并完成相應的任務. 古希臘的幾何學家海倫在他的《度量》一書中給出了利用三角形的三邊求三角形面積的“海倫公式”:如果一個三角形的三邊長分別為a、b、c,設p= ![]() ,則三角形的面積S=
,則三角形的面積S= ![]() .
.
我國南宋著名的數學家秦九韶,曾提出利用三角形的三邊求面積的“秦九韶公式”(三斜求積術):如果一個三角形的三邊長分別為a、b、c,則三角形的面積S= ![]() .
.
(1)若一個三角形的三邊長分別是5,6,7,則這個三角形的面積等于 .
(2)若一個三角形的三邊長分別是 ![]() ,求這個三角形的面積.
,求這個三角形的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
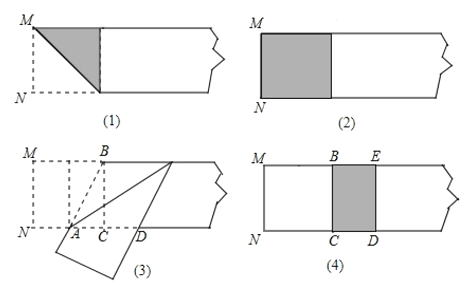
【題目】我們做個折紙游戲:第一步:在一張矩形紙片的一端,利用圖![]() 的方法折出一個正方形,然后把紙片展開;第二步:如圖
的方法折出一個正方形,然后把紙片展開;第二步:如圖![]() ,把這個正方形折成兩個相等的矩形,再把紙片展開;第三步:折出內側矩形的對角線
,把這個正方形折成兩個相等的矩形,再把紙片展開;第三步:折出內側矩形的對角線![]() ,并把它折到圖
,并把它折到圖![]() 中所示的
中所示的![]() 處;第四步:如圖
處;第四步:如圖![]() , 展平紙片,按照所得的
, 展平紙片,按照所得的![]() 點折出
點折出![]() .則矩形
.則矩形![]() 的寬
的寬![]() 與長
與長![]() 的比是__________.
的比是__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:已知AB∥CD,∠ABE與∠CDE兩個角的角平分線相交于F.
(1)如圖1,若∠E=80°,求∠BFD的度數.
(2)如圖2:若∠ABM=![]() ∠ABF,∠CDM=
∠ABF,∠CDM=![]() ∠CDF,寫出∠M和∠E之間的數量關系并證明你的結論.
∠CDF,寫出∠M和∠E之間的數量關系并證明你的結論.
(3)若∠ABM=![]() ∠ABF, ∠CDM=
∠ABF, ∠CDM=![]() ∠CDF, 設∠E=m°,直接用含有n、m°的代數式寫出∠M= (不寫過程)
∠CDF, 設∠E=m°,直接用含有n、m°的代數式寫出∠M= (不寫過程)

查看答案和解析>>
科目:初中數學 來源: 題型:
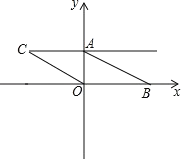
【題目】如圖.已知在平面直角坐標系中.點 A(0,m),點 B(n,0),D(2m,n),且 m、n 滿足(m﹣2)2+![]() =0,將線段AB向左平移,使點B與點 O重合,點C與點A對應.
=0,將線段AB向左平移,使點B與點 O重合,點C與點A對應.
(1)求點C、D的坐標;
(2)連接CD,動點P從點O出發,以每秒1個單位的速度,沿射線OB方向運動,設點P運動時間為t秒,是否存在某一時刻,使 SPCD=4SAOB,若存在,請求出t值,并寫出P點坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在 ABCD中,CD=2AD,BE⊥AD于點E,F為DC的中點,連結EF、BF,下列結論:①∠ABC=2∠ABF;②EF=BF;③S四邊形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正確結論的個數共有( ).

A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com