
【題目】如圖,矩形ABCD中,P為AD上一點,將△ABP沿BP翻折至△EBP,點A與點E重合;
(1)如圖1,若AB=10,BC=6,點E落在CD邊上,求AP的長;
(2)如圖2,若AB=8,BC=6, PE與CD相交于點O,且OE=OD,求AP的長;
(3)如圖3,若AB=4,BC=6,點P是AD的中點,求DE的長.

【答案】(1)![]() (2)4.8(3)3.6
(2)4.8(3)3.6
【解析】試題分析:(1)在Rt△BCE中,BC=6,BE=AB=10,根據勾股定理求出CE的值為8,則DE=10-8=2,設AP=x,則PE=x,DP=6-x,在Rt△DPE中,根據勾股定理得出方程,解方程即可;
(2)由折疊的性質得出EP=AP,∠E=∠A=90°,BE=AB=8,由ASA證明△ODP≌△OEG,得出OP=OG,PD=GE,設AP=EP=x,則PD=GE=6-x,DG=x,求出CG、BG,根據勾股定理得出方程,解方程即可;
(3)以點A為原點建立平面直角坐標系,則點A(0,0),B(4,0),C(4,6),D(0,6),P(0,3),設點E的坐標為(x,y),根據PE=PA=3可得,PE=![]() ,BE=
,BE=![]() ,解得y=
,解得y= ![]() ,再將y=
,再將y= ![]() 代入
代入![]() 中得,x(
中得,x(![]() )=0,所以x=0或x=
)=0,所以x=0或x=![]() ,所以y=
,所以y=![]() ,再根據DE=
,再根據DE=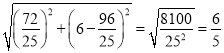 ;
;
試題解析:
(1)∵△ABP沿BP翻折至△EBP,點A與點E重合,AB=10,
∴BE=AB=10,PE=AP,
∴在Rt△BCE中,CE=![]() ,
,
∴DE=CD-CE=2,
設AP=x,則DP=6-x
∵在Rt△DPE中,DP2+DE2=PE2,
∴(6-x)2+22=x2,
∴x=![]() ;
;
(2)∵四邊形ABCD是矩形,
∴∠D=∠A=∠C=90°,AD=BC=6,CD=AB=8,
根據題意得:△ABP≌△EBP,
∴EP=AP,∠E=∠A=90°,BE=AB=8,
在△ODP和△OEG中,
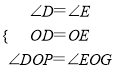
∴△ODP≌△OEG(ASA),
∴OP=OG,PD=GE,
∴DG=EP,
設AP=EP=x,則PD=GE=6-x,DG=x,
∴CG=8-x,BG=8-(6-x)=2+x,
根據勾股定理得:BC2+CG2=BG2,
即62+(8-x)2=(x+2)2,
解得:x=4.8,
∴AP=4.8;
(3)以點A為原點建立平面直角坐標系,則點A(0,0),B(4,0),C(4,6),D(0,6),P(0,3),設點E的坐標為(x,y),根據PE=PA=3可得,
PE=![]() ,BE=
,BE=![]() ,
,
解得y= ![]() ,
,
把y= ![]() 代入
代入![]() 中得,
中得,
x(![]() )=0,
)=0,
所以x=0(舍去)或x=![]() ,
,
所以y=![]() ,
,
∴DE=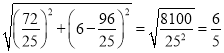 ;
;


 新課標快樂提優暑假作業陜西旅游出版社系列答案
新課標快樂提優暑假作業陜西旅游出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,己知△ABC中,∠C=90°,∠A=30°,AC=![]() .動點D在邊AC上,以BD為邊作等邊△BDE(點E、A在BD的同側).在點D從點A移動至點C的過程中,點E移動的路線長為 .
.動點D在邊AC上,以BD為邊作等邊△BDE(點E、A在BD的同側).在點D從點A移動至點C的過程中,點E移動的路線長為 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校國旗護衛隊成員的身高分布加下表:
身高/cm | 159 | 160 | 161 | 162 |
人數 | 7 | 10 | 9 | 9 |
則學校國旗護衛隊成員的身高的眾數和中位數分別是( )
A.160和160B.160和160.5C.160和161D.161和161
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從泰州到某市,可乘坐普通列車或動車,已知動車的行駛路程是400千米,普通列車的行駛路程是動車的行駛路程的1.3倍.
(1)求普通列車的行駛路程;
(2)若動車的平均速度(千米/時)是普通列車平均速度(千米/時)的2.5倍,且乘坐動車所需時間比乘坐普通列車所需時間縮短3小時,求動車的平均速度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】九年級一班數學老師對全班學生在模擬考試中A卷成績進行統計后,制成如下的統計表:
成績(分) | 80 | 82 | 84 | 86 | 87 | 90 |
人數 | 8 | 12 | 9 | 3 | 5 | 8 |
則該班學生A卷成績的眾數和中位數分別是( )
A. 82分,82分 B. 82分,83分 C. 80分,82分 D. 82分,84分
查看答案和解析>>
科目:初中數學 來源: 題型:
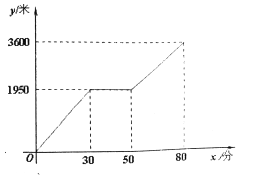
【題目】小穎和小亮上山游玩,小顆乘坐纜車,小亮步行,兩人相約在山頂的纜車終點會合.已知小亮行走到纜車終點的路程是纜車到山頂的線路長的2倍,小顆在小亮出發后50分才乘上纜車,纜車的平均速度為180米/分,設小亮出發x分后行走的路程為y米。圖中的折線表示小亮在整個行走過程中y隨x的變化關系.
(1)小亮行走的總路程是_________米,他途中休息了___________分;
(2)分別求出小亮在休息前和休息后所走的路程段上的步行速度;
(3)當小穎到達纜車終點時,小亮離纜車終點的路程是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AD是等腰△ABC底邊BC上的高.點O是AC中點,延長DO到E,使OE=OD,連接AE,CE.
(1)求證:四邊形ADCE的是矩形;
(2)若AB=17,BC=16,求四邊形ADCE的面積.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com