
【題目】已知x=m時,多項式x2+2x+n2的值為﹣1,則x=﹣m時,該多項式的值為 .
【答案】3
【解析】解:∵多項式x2+2x+n2=(x+1)2+n2﹣1,
∵(x+1)2≥0,n2≥0,
∴(x+1)2+n2﹣1的最小值為﹣1,
此時m=﹣1,n=0,
∴x=﹣m時,多項式x2+2x+n2的值為m2﹣2m+n2=3
所以答案是:3.
或解:∵多項式x2+2x+n2的值為﹣1,
∴x2+2x+1+n2=0,
∴(x+1)2+n2=0,
∵(x+1)2≥0,n2≥0,
∴ ![]() ,
,
∴x=m=﹣1,n=0,
∴x=﹣m時,多項式x2+2x+n2的值為m2﹣2m+n2=3
所以答案是:3.
【考點精析】解答此題的關鍵在于理解代數式求值的相關知識,掌握求代數式的值,一般是先將代數式化簡,然后再將字母的取值代入;求代數式的值,有時求不出其字母的值,需要利用技巧,“整體”代入.


科目:初中數學 來源: 題型:
【題目】一張長方形的桌子可坐6人,按下圖將桌子拼起來.

按這樣規律做下去:(1)有5張桌子時可坐 人;
(2)有10張桌子時可坐 人;
(3)有n張桌子可以坐 人(用含有n的代數式表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把2張形狀大小完全相同的小長方形卡片(如圖①)不重疊地放在一個底面為長方形(長為m,寬為n)的盒子底部(如圖②),盒子底面未被卡片覆蓋的部分用陰影表示.陰影部分剛好能分割成兩張形狀大小不同的小長方形卡片(如圖③),則分割后的兩個陰影長方形的周長和是( )
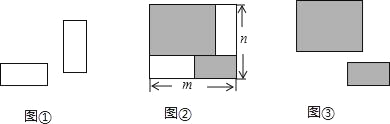
A. 4mB. 2(m+n)C. 4nD. 4(m﹣n)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有若干個數,第一個數記為a1,第2個數記為a2,第3個數記為a3,……,第n個數記為an,若a1=﹣![]() ,從第二個數起,每一個數都是“1”與它前面那個數的差的倒數.
,從第二個數起,每一個數都是“1”與它前面那個數的差的倒數.
(1)直接寫出a2,a3,a4的值;
(2)根據以上結果,計算a1+a2+a3+…+a2017+a2018.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠AOB=120°,OP平分∠AOB,且OP=2.若點M,N分別在OA,OB上,且△PMN為等邊三角形,則滿足上述條件的△PMN有( )

A. 2個 B. 3個 C. 4個 D. 無數個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】熱氣球的探測器顯示,從熱氣球A看一棟樓頂部B的仰角α為45°,看這棟樓底部C的俯角β為60°,熱氣球與樓的水平距離為100m,求這棟樓的高度(結果保留根號).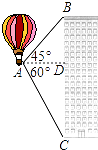
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將一張長方形的紙對折(使寬邊重合,然后再對折),第一次對折,得到一條折痕連同長方形的兩條寬邊共3條等寬線(如圖(1),第二次對折(每次的折痕與上次的折痕保持平行),得到5條等寬線(如圖(2)所示),連續對折三次后,可以得到9條等寬線(如圖(3所示),對折四次可以得到17條等寬線,如果對折6次,那么可以得到的等寬線條數是______條.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com