
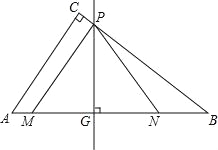
【題目】如圖,在Rt△ABC中,∠ACB=90°,AC=6,BC=8.動點M從點A出發,以每秒1個單位長度的速度沿AB向點B勻速運動;同時,動點N從點B出發,以每秒3個單位長度的速度沿BA向點A勻速運動.過線段MN的中點G作邊AB的垂線,垂足為點G,交△ABC的另一邊于點P,連接PM、PN,當點N運動到點A時,M、N兩點同時停止運動,設運動時間為t秒.
(1)當t= 秒時,動點M、N相遇;
(2)設△PMN的面積為S,求S與t之間的函數關系式.
【答案】(1)2.5
(2)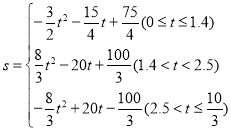
【解析】
試題分析:(1)根據勾股定理可得AB=10,若動點M、N相遇,則有t+3t=10,即可求出t的值;
(2)由于“點P在BC上”與“點P在點AC上”及“點M在點N的左邊”與“點M在點N的右邊”對應的MN、PG的表達式不同,S與t之間的函數關系式也就不同,因此需分情況討論.只需先考慮臨界位置(點P與點C重合,點M與點N重合、點N與點A重合)所對應的t的值,然后分三種情況(①0≤t≤1.4,②1.4<t<2.5,③2.5<t≤![]() )討論,用t的代數式表示出MN和PG,就可解決問題.
)討論,用t的代數式表示出MN和PG,就可解決問題.
試題解析:(1)∵∠ACB=90°,AC=6,BC=8,∴AB=10,
∴t+3t=10,解得t=2.5(s),
即當t=2.5秒時,動點M,N相遇;
故答案為2.5;
(2)過點C作CH⊥AB于H,
由S△ABC=![]() ACBC=
ACBC=![]() ABCH得,CH=
ABCH得,CH=![]() =4.8,
=4.8,
∴AH=![]() =3.6,BH=10﹣3.6=6.4.
=3.6,BH=10﹣3.6=6.4.
∵當點N運動到點A時,M,N兩點同時停止運動,∴0≤t≤![]() .
.
當0≤t<2.5時,點M在點N的左邊,如圖1、圖2,
MN=AB﹣AM﹣BN=10﹣t﹣3t=10﹣4t.
∵點G是MN的中點,∴MG=![]() MN=5﹣2t,
MN=5﹣2t,
∴AG=AM+MG=t+5﹣2t=5﹣t,
∴BG=10﹣(5﹣t)=t+5.
當點P與點C重合時,點G與點H重合,
則有5﹣t=3.6,解得t=1.4.
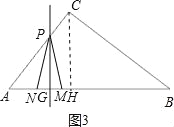
當2.5<t≤![]() 時,點M在點N右邊,如圖3,
時,點M在點N右邊,如圖3,
∵MN=AM﹣AN=AM﹣(AB﹣BN)=t﹣(10﹣3t)=4t﹣10,
∴NG=![]() MN=2t﹣5,
MN=2t﹣5,
∴AG=AN+NG=10﹣3t+2t﹣5=5﹣t.
綜上所述:①當0≤t≤1.4時,點M在點N的左邊,點P在BC上,如圖1,
此時MN=10﹣4t,BG=t+5,PG=BGtanB=![]() (t+5)=
(t+5)=![]() t+
t+![]() ,
,
∴S=![]() MNPG=
MNPG=![]() (10﹣4t)(
(10﹣4t)(![]() t+
t+![]() )=﹣
)=﹣![]() t2﹣
t2﹣![]() t+
t+![]() ;
;
②當1.4<t<2.5時,點M在點N的左邊,點P在AC上,如圖2,
此時MN=10﹣4t,AG=5﹣t,PG=AGtanA=![]() (5﹣t)=
(5﹣t)=![]() ﹣
﹣![]() t,
t,
∴S=![]() MNPG=
MNPG=![]() (10﹣4t)(
(10﹣4t)(![]() ﹣
﹣![]() t)=
t)=![]() t2﹣20t+
t2﹣20t+![]() ;
;
③當2.5<t≤![]() 時,點M在點N的右邊,點P在AC上,如圖3,
時,點M在點N的右邊,點P在AC上,如圖3,
此時MN=4t﹣10,AG=5﹣t,PG=AGtanA=![]() (5﹣t)=
(5﹣t)=![]() ﹣
﹣![]() t,
t,
∴S=![]() MNPG=
MNPG=![]() (4t﹣10)(
(4t﹣10)(![]() ﹣
﹣![]() t)=﹣
t)=﹣![]() t2+20t﹣
t2+20t﹣![]() ;
;
∴S與t之間的函數關系式為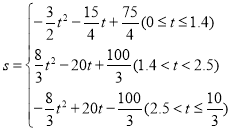 .
.




 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案 暑假作業安徽少年兒童出版社系列答案
暑假作業安徽少年兒童出版社系列答案科目:初中數學 來源: 題型:
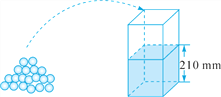
【題目】水平放置的容器內原有210 mm高的水,如圖,將若干個球逐一放入該容器中,每放入一個大球水面就上升4 mm,每放入一個小球水面就上升3 mm,假定放入容器中的所有球完全浸沒水中且水不溢出.設水面高為y(mm).
(1)若只放入大球,且個數為x大,求y關于x大的函數表達式(不必寫出x大的取值范圍).
(2)若放入6個大球后,開始放入小球,且小球個數為x小.
①求y關于x小的函數表達式(不必寫出x小的取值范圍).
②若限定水面高不超過260 mm,則最多能放入幾個小球?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知某公司前年繳稅40萬元,今年繳稅48.4萬元,求該公司這兩年繳稅的年平均增長率.設該公司這兩年繳稅的年平均增長率為x,根據題意,可列方程為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】.在農村電網改造中,四個自然村分別位于如圖所示的A,B,C,D處,現計劃安裝一臺變壓器,使到四個自然村的輸電線路的總長最短,那么這個變壓器應安裝在AC,BD的交點E處,你知道這是為什么嗎?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在一次軍事演習中,藍方在一條東西走向的公路上的A處朝正南方向撤退,紅方在公路上的B處沿南偏西60°方向前進實施攔截,紅方行駛1000米到達C處后,因前方無法通行,紅方決定調整方向,再朝南偏西45°方向前進了相同的距離,剛好在D處成功攔截藍方,求攔截點D處到公路的距離(結果不取近似值).

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com