
【題目】如圖,在△ACE中,CA=CE,∠CAE=30°,⊙O經過點C,且圓的直徑AB在線段AE上.
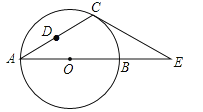
(1)試說明CE是⊙O的切線;
(2)若△ACE中AE邊上的高為h,試用含h的代數式表示⊙O的直徑AB;
(3)設點D是線段AC上任意一點(不含端點),連接OD,當![]() CD+OD的最小值為6時,求⊙O的直徑AB的長.
CD+OD的最小值為6時,求⊙O的直徑AB的長.
【答案】(1)證明見試題解析;(2)AB= ![]() ;(3)
;(3)![]() .
.
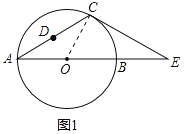
【解析】試題分析:(1)連接OC,如圖1,要證CE是⊙O的切線,只需證∠OCE=90°即可;
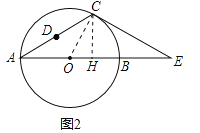
(2)過點C作CH⊥AB于H,連接OC,如圖2,在Rt△OHC中運用三角函數即可;
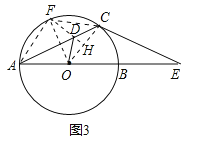
(3)作OF平分∠AOC,交⊙O于F,連接AF、CF、DF,如圖3,先證四邊形AOCF是菱形,由對稱性可得DF=DO.過點D作DH⊥OC于H,易得DH=![]() DC,從而有
DC,從而有![]() CD+OD=DH+FD.根據兩點之間線段最短可得:當F、D、H三點共線時,DH+FD(即
CD+OD=DH+FD.根據兩點之間線段最短可得:當F、D、H三點共線時,DH+FD(即![]() CD+OD)最小,然后在Rt△OHF中運用三角函數即可解決問題.
CD+OD)最小,然后在Rt△OHF中運用三角函數即可解決問題.
試題解析:(1)連接OC,如圖1,∵CA=CE,∠CAE=30°,∴∠E=∠CAE=30°,∠COE=2∠A=60°,∴∠OCE=90°,∴CE是⊙O的切線;
(2)過點C作CH⊥AB于H,連接OC,如圖2,由題可得CH=h,在Rt△OHC中,CH=OCsin∠COH,∴h=OCsin60°=![]() OC,∴OC=
OC,∴OC=![]() =
= ![]() ,∴AB=2OC=
,∴AB=2OC= ![]() ;
;
(3)作OF平分∠AOC,交⊙O于F,連接AF、CF、DF,如圖3,則∠AOF=∠COF=![]() ∠AOC=
∠AOC=![]() (180°﹣60°)=60°,∵OA=OF=OC,∴△AOF、△COF是等邊三角形,∴AF=AO=OC=FC,∴四邊形AOCF是菱形,∴根據對稱性可得DF=DO,過點D作DH⊥OC于H,∵OA=OC,∴∠OCA=∠OAC=30°,∴DH=DCsin∠DCH=DCsin30°=
(180°﹣60°)=60°,∵OA=OF=OC,∴△AOF、△COF是等邊三角形,∴AF=AO=OC=FC,∴四邊形AOCF是菱形,∴根據對稱性可得DF=DO,過點D作DH⊥OC于H,∵OA=OC,∴∠OCA=∠OAC=30°,∴DH=DCsin∠DCH=DCsin30°=![]() DC,∴
DC,∴![]() CD+OD=DH+FD.根據兩點之間線段最短可得:當F、D、H三點共線時,DH+FD(即
CD+OD=DH+FD.根據兩點之間線段最短可得:當F、D、H三點共線時,DH+FD(即![]() CD+OD)最小,此時FH=OFsin∠FOH=
CD+OD)最小,此時FH=OFsin∠FOH=![]() OF=6,則OF=
OF=6,則OF=![]() ,AB=2OF=
,AB=2OF=![]() ,∴當
,∴當![]() CD+OD的最小值為6時,⊙O的直徑AB的長為
CD+OD的最小值為6時,⊙O的直徑AB的長為![]() .
.


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:初中數學 來源: 題型:
【題目】老師在黑板上書寫了一個正確的演算過程,隨后用手掌捂住了一個多項式,形式如下:
![]()
(1)求所捂的多項式;
(2)若x為正整數,任取x的幾個值并求出所捂多項式的值,你能發現什么規律?
(3)若所捂多項式的值為144,請直接寫出正整數x的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
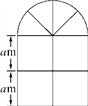
【題目】(12分)如圖是某種窗戶的形狀,其上部是半圓形,下部是邊長相同的四個小正方形,已知下部的小正方形的邊長為am,計算:
(1)窗戶的面積;
(2)窗框的總長;
(3)若a=1,窗戶上安裝的是玻璃,玻璃每平方米25元,窗框每米20元,窗框的厚度不計,求制作這種窗戶需要的費用是多少元(π取3.14,結果保留整數).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道,對于一個圖形,通過兩種不同的方法計算它的面積,可以得到一個數學等式.例如圖![]() 可以得到
可以得到![]()
![]() .請解答下列問題:
.請解答下列問題:

(1)寫出圖![]() 中所表示的數學等式;
中所表示的數學等式;

(2)利用(1)中所得到的結論,解決下面的問題:已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)小明同學打算用![]() 張邊長為
張邊長為![]() 的正方形,
的正方形,![]() 張邊長為
張邊長為![]() 的正方形,
的正方形,![]() 張相鄰兩邊長為分別為
張相鄰兩邊長為分別為![]() 、
、![]() 的長方形紙片拼出了一個面積為
的長方形紙片拼出了一個面積為 ![]() 長方形,那么他總共需要多少張紙片?
長方形,那么他總共需要多少張紙片?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對連續的偶數2,4,6,8,…排成如圖的形式.若將圖中的十字框上下左右移動,框住的五個數之和能等于2020嗎?若能,請寫出這五個數中位置在最中間的數;若不能,請說明理由.你的答案是:____________________________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算
(1)(-![]() )+(+
)+(+![]() )-(-
)-(-![]() )+(-
)+(-![]() )
)
(2)-54×![]() ÷(-
÷(-![]() )×
)×![]()
(3)-29×![]() -(-
-(-![]() )+29×(-
)+29×(-![]() )
)
(4)(-![]() -
-![]() +
+![]() )÷(-
)÷(-![]() )
)
(5)-42+3×(-2)2+(-6)÷(-![]() )2
)2
(6)∣-![]() ∣÷(
∣÷(![]() -
-![]() )-
)-![]() ×(-4)2
×(-4)2
查看答案和解析>>
科目:初中數學 來源: 題型:
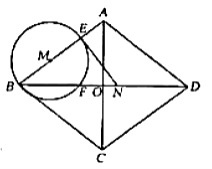
【題目】如圖,菱形![]() 中,對角線
中,對角線![]() 相交于點
相交于點![]() ,
,![]() ,動點
,動點![]() 從點
從點![]() 出發,沿線段
出發,沿線段![]() 以
以![]() 的速度向點
的速度向點![]() 運動,同時動點
運動,同時動點![]() 從點
從點![]() 出發,沿線段
出發,沿線段![]() 以
以![]() 的速度向點
的速度向點![]() 運動,當其中一個動點停止運動時另一個動點也隨之停止.設運動時間為
運動,當其中一個動點停止運動時另一個動點也隨之停止.設運動時間為![]() ,以點
,以點![]() 為圓心,
為圓心,![]() 為半徑的⊙
為半徑的⊙![]() 與射線
與射線![]() ,線段
,線段![]() 分別交于點
分別交于點![]() ,連接
,連接![]() .
.
(1)求![]() 的長(用含有
的長(用含有![]() 的代數式表示),并求出
的代數式表示),并求出![]() 的取值范圍;
的取值范圍;
(2)當![]() 為何值時,線段
為何值時,線段![]() 與⊙
與⊙![]() 相切?
相切?
(3)若⊙![]() 與線段
與線段![]() 只有一個公共點,求
只有一個公共點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
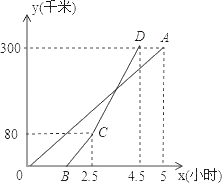
【題目】甲、乙兩地相距300千米,一輛貨車和一輛轎車先后從甲地出發向乙地,如圖,線段OA表示貨車離甲地距離y(千米)與時間x(小時)之間的函數關系;折線BCD表示轎車離甲地距離y(千米)與x(小時)之間的函數關系.請根據圖象解答下列問題:
(1)轎車到達乙地后,貨車距乙地多少千米?
(2)求線段CD對應的函數解析式.
(3)轎車到達乙地后,馬上沿原路以CD段速度返回,求貨車從甲地出發后多長時間再與轎車相遇(結果精確到0.01).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)請根據下列計算,把解題過程補充完整,并把解題過程中用到的運算律寫在題后的橫線上:
①![]()
解:原式![]()
![]()
![]()
![]()
![]()
![]() .
.
運算律: .
②![]() .
.
解:原式![]()
![]()
![]()
![]() )
)![]() (
( ![]()
![]()
![]()
![]()
運算律: .
(2)計算下列各題:
①![]()
②![]()
③![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com