
【題目】隨著某市養老機構(養老機構指社會福利院、養老院、社區養老中心等)建設穩步推進,擁有的養老床位不斷增加.
(1)該市的養老床位數從2013年底的2萬個增長到2015年底的2.88萬個,求該市這兩年(從2013年度到2015年底)擁有的養老床位數的平均年增長率;
(2)若該市某社區今年準備新建一養老中心,其中規劃建造三類養老專用房間共100間,這三類養老專用房間分別為單人間(1個養老床位),雙人間(2個養老床位),三人間(3個養老床位),因實際需要,單人間房間數在10至30之間(包括10和30),且雙人間的房間數是單人間的2倍,設規劃建造單人間的房間數為t.
①若該養老中心建成后可提供養老床位200個,求t的值;
②求該養老中心建成后最多提供養老床位多少個?最少提供養老床位多少個?
【答案】(1)20%;(2)①25;②該養老中心建成后最多提供養老床位260個,最少提供養老床位180個.
【解析】
試題分析:(1)設該市這兩年(從2013年度到2015年底)擁有的養老床位數的平均年增長率為x,根據“2015年的床位數=2013年的床位數×(1+增長率)的平方”可列出關于x的一元二次方程,解方程即可得出結論;
(2)①設規劃建造單人間的房間數為t(10≤t≤30),則建造雙人間的房間數為2t,三人間的房間數為100﹣3t,根據“可提供的床位數=單人間數+2倍的雙人間數+3倍的三人間數”即可得出關于t的一元一次方程,解方程即可得出結論;
②設該養老中心建成后能提供養老床位y個,根據“可提供的床位數=單人間數+2倍的雙人間數+3倍的三人間數”即可得出y關于t的函數關系式,根據一次函數的性質結合t的取值范圍,即可得出結論.
試題解析:(1)設該市這兩年(從2013年度到2015年底)擁有的養老床位數的平均年增長率為x,由題意可列出方程:![]()
解得:![]() =0.2=20%,
=0.2=20%,![]() =﹣2.2(不合題意,舍去).
=﹣2.2(不合題意,舍去).
答:該市這兩年擁有的養老床位數的平均年增長率為20%.
(2)①設規劃建造單人間的房間數為t(10≤t≤30),則建造雙人間的房間數為2t,三人間的房間數為100﹣3t,由題意得:t+4t+3(100﹣3t)=200,解得:t=25.
答:t的值是25.
②設該養老中心建成后能提供養老床位y個,由題意得:y=t+4t+3(100﹣3t)=﹣4t+300(10≤t≤30),∵k=﹣4<0,∴y隨t的增大而減小.
當t=10時,y的最大值為300﹣4×10=260(個),當t=30時,y的最小值為300﹣4×30=180(個).
答:該養老中心建成后最多提供養老床位260個,最少提供養老床位180個.


科目:初中數學 來源: 題型:
【題目】現有若干張如圖1所示的正方形紙片A,B和長方形紙片C.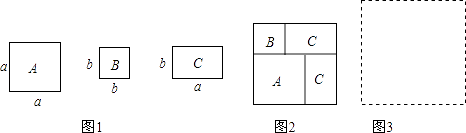
(1)小王利用這些紙片拼成了如圖2的一個新正方形,通過用兩種不同的方法計算新正方形面積,由此,他得到了一個等式:;
(2)小王再取其中的若干張紙片(三種紙片都要取到)拼成一個面積為a2+3ab+nb2的長方形,則n可取的正整數值是 , 并請你在圖3位置畫出拼成的長方形;
(3)根據拼圖經驗,請將多項式a2+5ab+4b2分解因式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列計算中正確的是( )
A. (x+2)2=x2+2x+4 B. (-3-x)(3+x)=9-x2
C. (-3-x)(3+x)=-x2-9+6x D. (2x-3y)2=4x2+9y2-12xy
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一副三角板疊在一起如圖放置,最小銳角的頂點D恰好放在等腰直角三角形的斜邊上,AC與DM , DN分別交于點E , F , 把△DEF繞點D旋轉到一定位置,使得DE=DF , 則∠BDN的度數是( )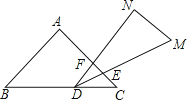
A.105°
B.115°
C.120°
D.135°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠A=70°,AC=BC , 以點B為旋轉中心把△ABC按順時針旋轉α度,得到△A′B′C , 點A′恰好落在AC上,連接CC′,則∠ACC′=.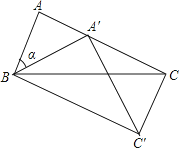
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,已知正方形ABCD中的△DCF可以經過旋轉得到△BCE .
①圖中哪一個點是旋轉中心?
②按什么方向旋轉了多少度?
③如果CF=3cm.求EF的長?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠ACB=90°,AC=BC , 點D在邊AB上,連接CD , 將線段CD繞點C順時針旋轉90°至CE位置,連接AE . 求證:AE=BD . 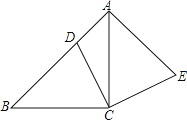
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在△ABC中,∠1=∠2,G是AD的中點,延長BG交AC于點E,F為AB上一點,CF⊥AD交AD于點H.①AD是△ABE的角平分線;②BE是△ABD的邊AD上的中線;③CH為△ACD的邊AD上的高;④AH是△ACF的角平分線和高線,其中判斷正確的有.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如表所示,從左到右在每個小格子中都填入一個整數,使得其中任意三個相鄰格子中所填整數之和都相等,則第2016個格子中的數為( ) ![]()
A.3
B.2
C.0
D.﹣1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com