
【題目】在平面直角坐標系xOy中,拋物線![]() 與y軸交于C點,與x軸交于A,B兩點(點A在點B左側),且點A的橫坐標為-1.
與y軸交于C點,與x軸交于A,B兩點(點A在點B左側),且點A的橫坐標為-1.
(1)求a的值;
(2)設拋物線的頂點P關于原點的對稱點為![]() ,求點
,求點![]() 的坐標;
的坐標;
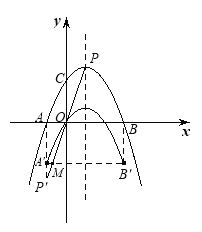
(3)將拋物線在A,B兩點之間的部分(包括A, B兩點),先向下平移3個單位,再向左平移m(![]() )個單位,平移后的圖象記為圖象G,若圖象G與直線
)個單位,平移后的圖象記為圖象G,若圖象G與直線![]() 無交點,求m的取值范圍
無交點,求m的取值范圍
【答案】(1)、a=-2;(2)、P′(-1,-4);(3)、m>![]()
【解析】
試題分析:(1)、將點A的坐標代入解析式求出a的值;(2)、根據a的值得出函數解析式,然后求出頂點坐標,根據原點對稱的性質求出點P′的坐標;(3)、根據題意得出直線PP′的解析式,圖象向下平移3個單位后,得出A′和B′的坐標,若圖象G與直線PP′無交點,則B′要左移到M及左邊,將y=3代入一次函數得出點M的坐標,然后求出m的取值范圍.
試題解析:(1)、∵A(-1,0)在拋物線![]() 上,∴
上,∴![]() ,∴解得
,∴解得![]()
(2)、∴拋物線表達式為![]() . ∴拋物線
. ∴拋物線![]() 的頂點P的坐標為(1,4).
的頂點P的坐標為(1,4).
∵點P關于原點的對稱點為![]() ,∴
,∴![]() 的坐標為(-1,-4).
的坐標為(-1,-4).
(3)、直線![]() 的表達式為
的表達式為![]() ,
,
圖象向下平移3個單位后,![]() 的坐標為(-1,-3),
的坐標為(-1,-3),![]() 的坐標為(3,-3),
的坐標為(3,-3),
若圖象G與直線![]() 無交點,則
無交點,則![]() 要左移到
要左移到![]() 及左邊,
及左邊,
令![]() 代入
代入![]() ,則
,則![]() ,
,![]() 的坐標為
的坐標為![]()
∴![]() ,∴
,∴![]() .
.


科目:初中數學 來源: 題型:
【題目】(1)如圖1,已知:在△ABC中,∠BAC=90°,AB=AC,直線m經過點A,BD⊥直線m, CE⊥直線m,垂足分別為點D、E.證明:DE=BD+CE.
(2)如圖2,將(1)中的條件改為:在△ABC中,AB=AC,D、A、E三點都在直線m上,并且有∠BDA=∠AEC=∠BAC=α,其中α為任意銳角或鈍角.請問結論DE=BD+CE是否成立?如成立,請你給出證明;若不成立,請說明理由.
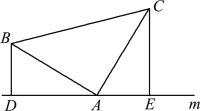
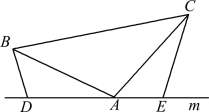
圖1 圖2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖1,拋物線的頂點為M,平行于x軸的直線與該拋物線交于點A,B(點A在點B左側),根據對稱性△AMB恒為等腰三角形,我們規定:當△AMB為直角三角形時,就稱△AMB為該拋物線的“完美三角形”.
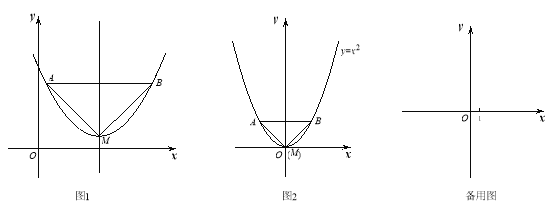
(1)①如圖2,求出拋物線![]() 的“完美三角形”斜邊AB的長;
的“完美三角形”斜邊AB的長;
②拋物線![]() 與
與![]() 的“完美三角形”的斜邊長的數量關系是 ;
的“完美三角形”的斜邊長的數量關系是 ;
(2)若拋物線![]() 的“完美三角形”的斜邊長為4,求a的值;
的“完美三角形”的斜邊長為4,求a的值;
(3)若拋物線![]() 的“完美三角形”斜邊長為n,且
的“完美三角形”斜邊長為n,且![]() 的最大值為-1,求m,n的值.
的最大值為-1,求m,n的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我國第一艘航母“遼寧艦”最大排水量為67500噸,用科學記數法表示這個數字是( )
A. 6.75×103噸 B. 7.5×103噸
C. 6.75×104噸 D. 6.75×105噸
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=x2﹣2mx﹣4(m>0)的頂點M關于坐標原點O的對稱點為M′,若點M′在這條拋物線上,則點M的坐標為( )
A.(1,﹣5)
B.(3,﹣13)
C.(2,﹣8)
D.(4,﹣20)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com