
【題目】如圖,直線![]() 交x軸于點A,交直線
交x軸于點A,交直線![]() 于點B(2,m).矩形CDEF的邊DC在x軸上,D在C的左側,EF在x軸的上方,DC=2,DE=4.當點C的坐標為(-2,0)時,矩形CDEF開始以每秒2個單位的速度沿x軸向右運動,運動時間為t秒.(注:矩形就是長方形)
于點B(2,m).矩形CDEF的邊DC在x軸上,D在C的左側,EF在x軸的上方,DC=2,DE=4.當點C的坐標為(-2,0)時,矩形CDEF開始以每秒2個單位的速度沿x軸向右運動,運動時間為t秒.(注:矩形就是長方形)
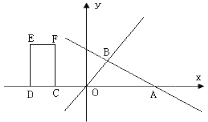
(1)求b、m的值;
(2)當矩形CDEF運動t秒時,請直接寫出C、D兩點的坐標(用含t的代數式表示)
(3)當點B在矩形CDEF的一邊上時,求t的值;
(4)設CF、DE分別交折線OBA于M、N兩點,當四邊形MCDN為直角梯形時,求t的取值范圍.
【答案】(1)b=4,m=3;(2)點C(2t![]() 2,0)、點D(2t
2,0)、點D(2t![]() 4,0);(3)當點B在矩形的一邊上時,t的值為2秒或3秒;(4)t的取值范圍為:2<t<5且t≠
4,0);(3)當點B在矩形的一邊上時,t的值為2秒或3秒;(4)t的取值范圍為:2<t<5且t≠![]() .
.
【解析】
(1)把B點坐標分別代入![]() 和
和![]() 可求出m,b.
可求出m,b.
(2)C點向右移動2t個單位,則C點的橫坐標要減2t,便可寫出C,D兩點坐標.
(3)首先判斷B點在EF的下方,再討論B點在DE或FC上,利用橫坐標相等求t.
(4)通過端點確定范圍,即C點到達A點,D點到達O點,還要去掉CM=DN時的t的值.
解:(1)把B(2,m)代入![]() ,得m=3.
,得m=3.
再把B(2,3)代入![]() ,得b=4.
,得b=4.
(2)因為點C向右移了2t個單位,則點C的橫坐標加2t,縱坐標還是0,
D點的橫坐標比點C要小2,
∴點C(2t-2,0)、點D(2t-4,0);
(3)∵3<4,
∴點B在EF的下方,不能在EF上,
點B在CF邊上時2t-2=2,解得:t=2,
點B在DE邊上時,2t-4=2,解得:t=3,
∴當點B在矩形的一邊上時,t的值為2秒或3秒;
(4)點D與O重合時,2t-4=0,解得:t=2,
點C與點A重合時,2t-2=8,解得t=5,
CF交AB于M,DE交BO于N時,M(2t-2,5-t),N(2t-4,3t-6),
當CM=DN時,即5-t=3t-6,
解得t=![]() ,
,
∴當t=![]() 時四邊形MCDN為矩形,
時四邊形MCDN為矩形,
∴當四邊形MCDN為直角梯形時,
t的取值范圍為:2<t<5且t≠![]() .
.


科目:初中數學 來源: 題型:
【題目】在△ABC中,AB=AC,BC=12,E為邊AC的中點,
(1)如圖1,過點E作EH⊥BC,垂足為點H,求線段CH的長;
(2)作線段BE的垂直平分線分別交邊BC、BE、AB于點D、O、F.
①如圖2,當∠BAC=90°時,求BD的長;
②如圖3,設tan∠ACB=x,BD=y,求y與x之間的函數表達式和tan∠ACB的最大值.

查看答案和解析>>
科目:初中數學 來源: 題型:
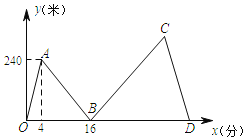
【題目】甲、乙兩人在筆直的湖邊公路上同起點、同終點、同方向勻速步行2400米,先到終點的人原地休息.已知甲先出發4分鐘,在整個步行過程中,甲、乙兩人間的距離y(米)與甲出發的時間x(分)之間的關系如圖中折線OA-AB-BC-CD所示.
(1)求線段AB的表達式,并寫出自變量x的取值范圍;
(2)求乙的步行速度;
(3)求乙比甲早幾分鐘到達終點?
查看答案和解析>>
科目:初中數學 來源: 題型:
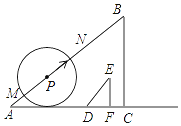
【題目】如圖,已知Rt△ABC的直角邊AC與Rt△DEF的直角邊DF在同一條直線上,且AC=60cm,BC=45cm,DF=6cm,EF=8cm.現將點C與點F重合,再以4cm/s的速度沿
CA方向移動△DEF;同時,點P從點A出發,以5cm/s的速度沿AB方向移動.設移動時間為t(s),以點P為圓心,3t(cm)長為半徑的⊙P與直線AB相交于點M,N,當點F與點A重合時,△DEF與點P同時停止移動,在移動過程中:
(1)連接ME,當ME∥AC時,t=________s;
(2)連接NF,當NF平分DE時,求t的值;
(3)是否存在⊙P與Rt△DEF的兩條直角邊所在的直線同時相切的時刻?若存在,求出t的值;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC的直角邊BC在x軸正半軸上,斜邊AC邊上的中線BD的反向延長線交y軸負半軸于點E,雙曲線![]() 的圖象經過點A,若S△BEC=3,則k等于( )
的圖象經過點A,若S△BEC=3,則k等于( )
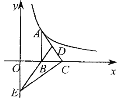
A.12B.6C.3D.2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學生的學業負擔過重會嚴重影響學生對待學習的態度.為此我市教育部門對部分學校的八年級學生對待學習的態度進行了一次抽樣調查(把學習態度分為三個層級,A級:對學習很感興趣;B級:對學習較感興趣;C級:對學習不感興趣),并將調查結果繪制成圖①和圖②的統計圖(不完整).請根據圖中提供的信息,解答下列問題:
(1)此次抽樣調查中,共調查了 名學生;
(2)將圖①補充完整;
(3)求出圖②中C級所占的圓心角的度數;
(4)根據抽樣調查結果,請你估計我市近8000名八年級學生中大約有多少名學生學習態度達標(達標包括A級和B級)?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,圖①是一個四邊形紙條 ABCD,其中 AB∥CD,E,F 分別為邊 AB,CD 上的兩個點,將紙條 ABCD 沿 EF 折疊得到圖②,再將圖②沿 DF 折疊得到圖③,若在圖③中,∠FEM=26°,則∠EFC 的度數為( )

A.52°B.64°C.102°D.128°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等邊三角形ABC中,AD⊥BC于點D,以AD為一邊向右作等邊三角形ADE,DE與AC交于點F.
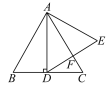
(1)試判斷DF與EF的數量關系,并給出證明;
(2)若CF的長為2 cm,試求等邊三角形ABC的邊長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題滿分8分)如圖,在△ABC中,AB=AC,∠DAC是△ABC的一個外角.
實踐與操作:
根據要求尺規作圖,并在圖中標明相應字母(保留作圖痕跡,不寫作法).

(1)作∠DAC的平分線AM;
(2)作線段AC的垂直平分線,與AM交于點F,與BC邊交于點E,連接AE、CF.
猜想并證明:
判斷四邊形AECF的形狀并加以證明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com