
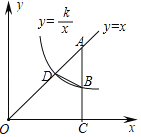
【題目】如圖,直線y=x與反比例函數(shù)y=![]() (x>0)的圖象相交于點D,點A為直線y=x上一點,過點A作AC⊥x軸于點C,交反比例函數(shù)y=
(x>0)的圖象相交于點D,點A為直線y=x上一點,過點A作AC⊥x軸于點C,交反比例函數(shù)y=![]() (x>0)的圖象于點B,連接BD.
(x>0)的圖象于點B,連接BD.
(1)若點B的坐標(biāo)為(8,2),則k= ,點D的坐標(biāo)為 ;
(2)若AB=2BC,且△OAC的面積為18,求k的值及△ABD的面積.
【答案】(1)16,(4,4);(2)12,12﹣![]()
【解析】
(1)由點B(8,2)在反比例函數(shù)![]() 的圖象上,代入可求k的值,將反比例函數(shù)的關(guān)系式與y=x聯(lián)立方程組,可以求出交點坐標(biāo),進(jìn)而確定點D的坐標(biāo);
的圖象上,代入可求k的值,將反比例函數(shù)的關(guān)系式與y=x聯(lián)立方程組,可以求出交點坐標(biāo),進(jìn)而確定點D的坐標(biāo);
(2)點A在直線y=x上,可知OC=AC,由△OAC的面積為18可求出AC的長,確定點A的坐標(biāo),由AB=2BC,可求AB、BC的長,確定點B的坐標(biāo),進(jìn)而求k得值,用(1)的方法可求點D的坐標(biāo),利用三角形的面積公式就可以求出三角形的面積.
解:(1)把B(8,2)代入![]() 得:k=2×8=16,
得:k=2×8=16,
∴反比例函數(shù)的關(guān)系式為![]() ,
,
由題意得: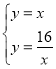
解得: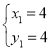 ,
, (舍去)
(舍去)
∴點D的坐標(biāo)為(4,4)
故答案為:16,(4,4)
(2)過點D作DE⊥OC,DF⊥AC,垂足為E、F,如圖所示:
∵點A在第一象限y=x上,
∴AC=OC,
又∵△OAC的面積為18,
∴AC=OC=6,
∵AB=2BC,
∴AB=4,BC=2,
∴點B(6,2),代入![]() 得,k=12;
得,k=12;
設(shè)點D(a,a)代入![]() 得,a=
得,a=![]() (a>0)
(a>0)
∴D(![]() ,
,![]() ),即OE=DE=
),即OE=DE=![]() ,
,
∴DF=EC=OC﹣OE=6﹣![]() ,
,
∴△ABD的面積=![]() ABDF=
ABDF=![]() ×4×(6﹣
×4×(6﹣![]() )=12﹣
)=12﹣![]() ;
;
因此k的值為12,∴△ABD的面積為12﹣![]() .
.



 同步練習(xí)河南大學(xué)出版社系列答案
同步練習(xí)河南大學(xué)出版社系列答案 同步練習(xí)西南大學(xué)出版社系列答案
同步練習(xí)西南大學(xué)出版社系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,圓心在坐標(biāo)原點的⊙O,與坐標(biāo)軸的交點分別為A、B和C、D.弦CM交OA于P,連結(jié)AM,已知tan∠PCO=![]() ,PC、PM是方程x2﹣px+20=0的兩根.
,PC、PM是方程x2﹣px+20=0的兩根.
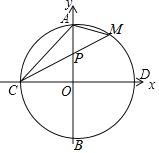
(1)求C點的坐標(biāo);
(2)寫出直線CM的函數(shù)解析式;
(3)求△AMC的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】下列命題為真命題的是( )
A.兩組身高數(shù)據(jù)的方差分別是![]() ,
,![]() ,那么乙組的身高比較整齊
,那么乙組的身高比較整齊
B.“明天下雨”是必然事件
C.一組數(shù)據(jù)3,5,4,5,6,7的眾數(shù)、中位數(shù)和平均數(shù)都是5
D.為了解某燈管的使用壽命,可以采用普查的方式進(jìn)行
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在矩形OABC中,點O為原點,點A的坐標(biāo)為(0,8),點C的坐標(biāo)為(6,0).拋物線y=﹣![]() x2+bx+c經(jīng)過點A、C,與AB交于點D.
x2+bx+c經(jīng)過點A、C,與AB交于點D.
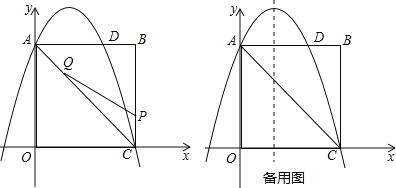
(1)求拋物線的函數(shù)解析式;
(2)點P為線段BC上一個動點(不與點C重合),點Q為線段AC上一個動點,AQ=CP,連接PQ,設(shè)CP=m,△CPQ的面積為S.
①求S關(guān)于m的函數(shù)表達(dá)式;
②當(dāng)S最大時,在拋物線y=﹣![]() x2+bx+c的對稱軸l上,若存在點F,使△DFQ為直角三角形,請直接寫出所有符合條件的點F的坐標(biāo);若不存在,請說明理由.
x2+bx+c的對稱軸l上,若存在點F,使△DFQ為直角三角形,請直接寫出所有符合條件的點F的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
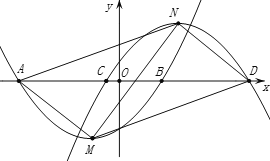
【題目】如圖,已知二次函數(shù)![]() 和二次函數(shù)
和二次函數(shù)![]() 圖象的頂點分別為M、N ,與x軸分別相交于A、B兩點(點A在點B的左邊)和C、D兩點(點C在點D的左邊),
圖象的頂點分別為M、N ,與x軸分別相交于A、B兩點(點A在點B的左邊)和C、D兩點(點C在點D的左邊),
(1))函數(shù)![]() 的頂點坐標(biāo)為 ;當(dāng)二次函數(shù)L1 ,L2 的
的頂點坐標(biāo)為 ;當(dāng)二次函數(shù)L1 ,L2 的![]() 值同時隨著
值同時隨著![]() 的增大而增大時,
的增大而增大時,![]() 的取值范圍是 ;
的取值范圍是 ;
(2)當(dāng)AD=MN時,求![]() 的值,并判斷四邊形AMDN的形狀(直接寫出,不必證明);
的值,并判斷四邊形AMDN的形狀(直接寫出,不必證明);
(3)當(dāng)B,C是線段AD的三等分點時,求a的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】足球運(yùn)動員將足球沿與地面成一定角度的方向踢出,足球飛行的路線是一條拋物線,不考慮空氣阻力,足球距離地面的高度![]() (單位:
(單位:![]() )與足球被踢出后經(jīng)過的時間
)與足球被踢出后經(jīng)過的時間![]() (單位:
(單位:![]() )之間的關(guān)系如下表:
)之間的關(guān)系如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列結(jié)論:①足球距離地面的最大高度為![]() ;②足球飛行路線的對稱軸是直線
;②足球飛行路線的對稱軸是直線![]() ;③足球被踢出
;③足球被踢出![]() 時落地;④足球被踢出
時落地;④足球被踢出![]() 時,距離地面的高度是
時,距離地面的高度是![]() .
.
其中正確結(jié)論的個數(shù)是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】閱讀以下材料:
材料一:如果兩個兩位數(shù)![]() 和
和![]() 將它們各自的十位數(shù)字和個位數(shù)字交換位置后得到兩個完全不同的新數(shù)
將它們各自的十位數(shù)字和個位數(shù)字交換位置后得到兩個完全不同的新數(shù)![]() ,
,![]() ,這兩個兩位數(shù)的乘積與交換后的兩個兩位數(shù)的乘積相等,則稱這樣的兩個兩位數(shù)為一對“有緣數(shù)對”.
,這兩個兩位數(shù)的乘積與交換后的兩個兩位數(shù)的乘積相等,則稱這樣的兩個兩位數(shù)為一對“有緣數(shù)對”.
例如:![]() ,所以,46和96是一對“有緣數(shù)對”,
,所以,46和96是一對“有緣數(shù)對”,
材料二:在進(jìn)行一些數(shù)學(xué)式計算時,我們可以把某一單項式或多項式看作一個整體,運(yùn)用整體換元,使得運(yùn)算更簡單.
例如:計算![]() ,令:
,令:![]() ,
,
原式![]()
![]()
解決如下問題:
(1)①請任寫一對“有緣數(shù)對”____________和____________.
②并探究“有緣數(shù)對”![]() 和
和![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 之間滿足怎樣的等量關(guān)系.并寫出證明過程.
之間滿足怎樣的等量關(guān)系.并寫出證明過程.
(2)若兩個兩位數(shù)![]() 與
與![]() 是一對“有緣數(shù)對,請求出這兩個兩位數(shù).
是一對“有緣數(shù)對,請求出這兩個兩位數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
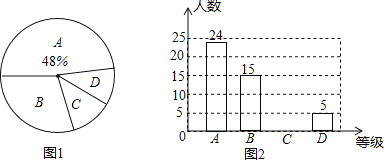
【題目】某銷售公司年終進(jìn)行業(yè)績考核,人事部門把考核結(jié)果按照A,B,C,D四個等級,繪制成兩個不完整的統(tǒng)計圖,如圖1,圖2.
![]() 參加考試的人數(shù)是______,扇形統(tǒng)計圖中D部分所對應(yīng)的圓心角的度數(shù)是______,請把條形統(tǒng)計圖補(bǔ)充完整;
參加考試的人數(shù)是______,扇形統(tǒng)計圖中D部分所對應(yīng)的圓心角的度數(shù)是______,請把條形統(tǒng)計圖補(bǔ)充完整;
![]() 若公司領(lǐng)導(dǎo)計劃從考核人員中選一人交流考核意見,求所選人員考核為A等級的概率;
若公司領(lǐng)導(dǎo)計劃從考核人員中選一人交流考核意見,求所選人員考核為A等級的概率;
![]() 為推動公司進(jìn)一步發(fā)展,公司決定計劃兩年內(nèi)考核A等級的人數(shù)達(dá)到30人,求平均每年的增長率
為推動公司進(jìn)一步發(fā)展,公司決定計劃兩年內(nèi)考核A等級的人數(shù)達(dá)到30人,求平均每年的增長率![]() 精確到
精確到![]() ,
,![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com