
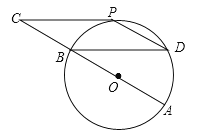
【題目】如圖,⊙O的直徑AB=12cm,C為AB延長線上一點,CP與⊙O相切于點P,過點B作弦BD∥CP,連接PD.
(1)求證:點P為![]() 的中點;
的中點;
(2)若∠C=∠D,求四邊形BCPD的面積.
【答案】(1)證明見解析;(2)![]() .
.
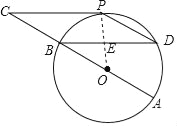
【解析】試題分析:(1)連接OP,根據切線的性質得到PC⊥OP,根據平行線的性質得到BD⊥OP,根據垂徑定理即可得到結論;
(2)根據圓周角定理得到∠POB=2∠D,根據三角形的內角和得到∠C=30°,推出四邊形BCPD是平行四邊形,于是得到結論.
試題解析:(1)連接OP,
∵CP與⊙O相切于點P,
∴PC⊥OP,
∵BD∥CP,
∴BD⊥OP,
∴![]() ,
,
∴點P為![]() 的中點;
的中點;
(2)∵∠C=∠D,
∵∠POB=2∠D,
∴∠POB=2∠C,
∵∠CPO=90°,
∴∠C=30°,
∵BD∥CP,
∴∠C=∠DBA,
∴∠D=∠DBA,
∴BC∥PD,
∴四邊形BCPD是平行四邊形,
∵PO=![]() AB=6,
AB=6,
∴PC=6![]() ,
,
∵∠ABD=∠C=30°,
∴OE=![]() OB=3,
OB=3,
∴PE=3,
∴四邊形BCPD的面積=PCPE=6![]() ×3=18
×3=18![]() .
.


 初中暑期銜接系列答案
初中暑期銜接系列答案科目:初中數學 來源: 題型:
【題目】在等腰三角形ABC中,AB=AC=10,BC=12,D為BC邊上的任意一點,過點D分別作DE⊥AB,DF⊥AC,垂足分別為E,F,則DE+DF=______.
查看答案和解析>>
科目:初中數學 來源: 題型:
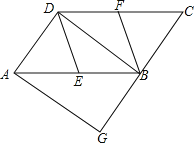
【題目】如圖,在平行四邊形ABCD中,E、F分別為邊AB、CD的中點,過A點作AG∥DB,交CB的延長線于點G.
(1)求證:DE∥BF;
(2)若∠G=90,求證:四邊形DEBF是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
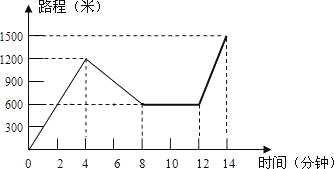
【題目】小紅星期天從家里出發騎車去舅舅家做客,當她騎了一段路時,想起要買個禮物送給表弟,于是又折回到剛經過的一家商店,買好禮物后又繼續騎車去舅舅家,以下是她本次去舅舅家所用的時間與路程的關系式示意圖.根據圖中提供的信息回答下列問題:
(1)小紅家到舅舅家的路程是______米,小紅在商店停留了______分鐘;
(2)在整個去舅舅家的途中哪個時間段小紅騎車速度最快,最快的速度是多少米/分
(3)本次去舅舅家的行程中,小紅一共行駛了多少米?一共用了多少分鐘?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(9分)已知:![]() ABCD的兩邊AB,AD的長是關于x的方程
ABCD的兩邊AB,AD的長是關于x的方程![]() 的兩個實數根.
的兩個實數根.
(1)當m為何值時,四邊形ABCD是菱形?求出這時菱形的邊長;
(2)若AB的長為2,那么![]() ABCD的周長是多少?
ABCD的周長是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】同學們都知道,![]() 表示5與
表示5與![]() 之差的絕對值,實際上也可以理解為5與
之差的絕對值,實際上也可以理解為5與![]() 兩數在數軸上所對應的兩點之間的距離.回答下列問題:
兩數在數軸上所對應的兩點之間的距離.回答下列問題:
(1)![]() _______.
_______.
(2)找出所有符合條件的整數![]() ,使得
,使得![]() 成立,這樣的整數是______.
成立,這樣的整數是______.
(3)對于任何有理數![]() ,
,![]() 的最小值是______.
的最小值是______.
(4)對于任何有理數![]() ,
,![]() 的最小值是_____,此時
的最小值是_____,此時![]() 的值是______.
的值是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖在平面直角坐標系中,將△ABO繞點A順時針旋轉到△AB1C1的位置,點B、O分別落在點B1、C1處,點B1在x軸上,再將△AB1C1繞點B1順時針旋轉到△A1B1C2的位置,點C2在x軸上,將△A1B1C2繞點C2順時針旋轉到△A2B2C2的位置,點A2在x軸上,依次進行下去…若點A(![]() ,0),B(0,2),則點B2018的坐標為( )
,0),B(0,2),則點B2018的坐標為( )

A. (6048,0)B. (6054,0)C. (6048,2)D. (6054,2)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() 是
是![]() 上的中線,
上的中線,![]() 的垂直平分線
的垂直平分線![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() 并延長交
并延長交![]() 于點
于點![]() ,
,![]() ,垂足為
,垂足為![]() .
.
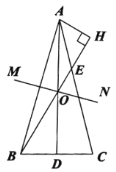
(1)求證:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的長;
的長;
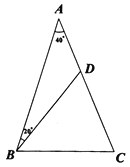
(3)如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 上的一點,且
上的一點,且![]() ,若
,若![]() ,請你直接寫出
,請你直接寫出![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店經銷一種泰山旅游紀念品,4月份的營業額為2000元,為擴大銷售量,5月份該商店對這種紀念品打9折銷售,結果銷售量增加20件,營業額增加700元.
(1)求該種紀念品4月份的銷售價格;
(2)若4月份銷售這種紀念品獲利800元,5月份銷售這種紀念品獲利多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com