【題目】如圖：在數軸上A點表示數
，B點示數
，C點表示數
，是最小的正整數，且、滿足
．
（1）=__________，=__________，=__________；
（2）若將數軸折疊，使得A點與C點重合，則點B與數__________表示的點重合；
（3）若點A、點B和點C分別以每秒2個單位、1個單位長度和4個單位長度的速度在數軸上同時向左運動，假設
秒鐘過后，A、B、C三點中恰有一點為另外兩點的中點，求的值；
（4）若點A、點B和點C分別以每秒2個單位、1個單位長度和4個單位長度的速度在數軸上同時向左運動時，小聰同學發現：當點C在B點右側時，
BC+3AB的值是個定值，求此時
的值．
【答案】（1）
=-3，
=1，
=9；（2）5；（3）1, 16, 4；（4）
=1．
【解析】
試題（1）根據非負數的意義求出a、c的值，根據最小的正整數求出b；
（2）根據對稱性可求解；
（3）分別以A、B、C為中點，分別求解即可；
（4）分別求出此時的BC、AB的長，然后由
BC+3AB可代入相應的速度值求解是定值的m.
試題解析：（1）因為b是最小的正整數，可得b=1，
根據
，求得=-3，=9；
（2）根據對稱性可求解：（-3+9）×2=3,
3-1=2,
3+2=5
答案為：5．
（3）B為中點時，
，
解得
=1,
A為中點時，
解得=16,
C為中點時，
解得=4；
（4）由題意可知，AB=4+t，
BC=8-3t
所以m·BC+3AB
=m·（8-3t）+3（4+t）
=8m+12-（3m-3）t
由定值可知3m-3=0
解得=1．
閱讀快車系列答案科目：初中數學 來源： 題型：
【題目】如圖，一次函數y=﹣
x+2分別交y軸、x軸于A，B兩點，拋物線y=﹣x2+bx+c過A，B兩點．
（1）求這個拋物線的解析式；
（2）作垂直于x軸的直線x=t，在第一象限交直線AB于M，交這個拋物線于N．求當t取何值時，△NAB的面積有最大值？最大值是多少？
（3）在（2）的情況下，以A、M、N、D為頂點作平行四邊形，求第四個頂點D的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】一位農民帶上若干千克自產的蘋果進城出售.為了方便，他帶了一些零錢備用，按市場價售出一些后，又降價出售，售出的蘋果
（千克）與他手中持有的錢數
（元）（含備用零錢）的關系如圖，結合圖象解決下列問題：
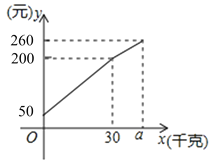
（1）農民自帶的零錢是多少？
（2）求出降價前每千克的蘋果價格是多少？
（3）降價后他按每千克
元將剩余蘋果售完，這時他手中
的錢（含備用零錢）是
元，試求出圖象中
的值；
（4）求出降價前與之間的關系式（不要求寫的取值范圍）.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知在平面直角坐標系xOy中，O是坐標原點，以P（1，1）為圓心的⊙P與x軸、y軸分別相切于點M和點N，點F從點M出發，沿x軸正方向以每秒1個單位長度的速度運動，連接PF，過點P作PE⊥PF交y軸于點E，設點F運動的時間是t秒（t＞0）
（1）若點E在y軸的負半軸上（如圖所示），求證：PE=PF；
（2）在點F運動過程中，設OE=a，OF=b，試用含a的代數式表示b；
（3）作點F關于點M的對稱點F′，經過M、E和F′三點的拋物線的對稱軸交x軸于點Q，連接QE．在點F運動過程中，是否存在某一時刻，使得以點Q、O、E為頂點的三角形與以點P、M、F為頂點的三角形相似？若存在，請直接寫出t的值；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
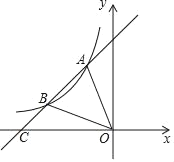
【題目】如圖，一次函數y＝ax+b的圖象與反比例函數y＝
圖象相交于點A（﹣1，2）與點B（﹣4，n）．
（1）求一次函數和反比例函數的解析式；
（2）求△AOB的面積．
（3）在第二象限內，求不等式ax+b＜的解集（請直接寫出答案）．
查看答案和解析>>
科目：初中數學 來源： 題型：
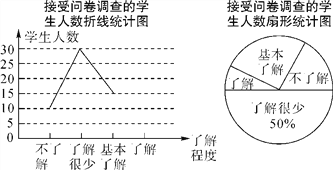
【題目】“校園安全”受到社會的廣泛關注，某校政教處對部分學生就校園安全知識的了解程度，進行了隨機抽樣調查，并繪制了如下兩幅尚不完整的統計圖．請你根據統計圖中所提供的信息解答下列問題：
(1)接受問卷調查的學生共有______名；
(2)請補全折線統計圖，并求出扇形統計圖中“基本了解”部分所對應扇形的圓心角的大小．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AB∥FC，D是AB上一點，DF交AC于點E，DE=FE，分別延長FD和CB交于點G．
（1）求證：△ADE≌△CFE；
（2）若GB=2，BC=4，BD=1，求AB的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某花店準備購進甲、乙兩種花卉，若購進甲種花卉20盆，乙種花卉50盆，需要720元；若購進甲種花卉40盆，乙種花卉30盆，需要880元．
（1）求購進甲、乙兩種花卉，每盆各需多少元？
（2）該花店銷售甲種花卉每盆可獲利6元，銷售乙種花卉每盆可獲利1元，現該花店準備拿出800元全部用來購進這兩種花卉，設購進甲種花卉x盆，全部銷售后獲得的利潤為W元，求W與x之間的函數關系式；
（3）在（2）的條件下，考慮到顧客需求，要求購進乙種花卉的數量不少于甲種花卉數量的6倍，且不超過甲種花卉數量的8倍，那么該花店共有幾種購進方案？在所有的購進方案中，哪種方案獲利最大？最大利潤是多少元？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com