
【題目】如圖,AB∥FC,D是AB上一點,DF交AC于點E,DE=FE,分別延長FD和CB交于點G.

(1)求證:△ADE≌△CFE;
(2)若GB=2,BC=4,BD=1,求AB的長.
科目:初中數學 來源: 題型:
【題目】四邊形ABCD是正方形,AC是對角線,E是平面內一點,且![]() ,過點C作
,過點C作![]() ,且
,且![]() 。連接AE、AF,M是AF的中點,作射線DM交AE于點N.
。連接AE、AF,M是AF的中點,作射線DM交AE于點N.
(1)如圖1,若點E,F分別在BC,CD邊上。
求證:①![]() ;
;
②![]() ;
;
(2)如圖2,若點E在四邊形ABCD內,點F在直線BC的上方,求![]() 與
與![]() 的和的度數。
的和的度數。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:在數軸上A點表示數![]() ,B點示數
,B點示數![]() ,C點表示數
,C點表示數![]() ,
,![]() 是最小的正整數,且
是最小的正整數,且![]() 、
、![]() 滿足
滿足![]() .
.
![]()
(1)![]() =__________,
=__________,![]() =__________,
=__________,![]() =__________;
=__________;
(2)若將數軸折疊,使得A點與C點重合,則點B與數__________表示的點重合;
(3)若點A、點B和點C分別以每秒2個單位、1個單位長度和4個單位長度的速度在數軸上同時向左運動,假設![]() 秒鐘過后,A、B、C三點中恰有一點為另外兩點的中點,求
秒鐘過后,A、B、C三點中恰有一點為另外兩點的中點,求![]() 的值;
的值;
(4)若點A、點B和點C分別以每秒2個單位、1個單位長度和4個單位長度的速度在數軸上同時向左運動時,小聰同學發現:當點C在B點右側時,![]() BC+3AB的值是個定值,求此時
BC+3AB的值是個定值,求此時![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知正方形OABC的邊長為2,頂點A,C分別在x軸,y軸的正半軸上,點E是BC的中點,F是AB延長線上一點且FB=1.

(1)求經過點O,A,E三點的拋物線解析式;
(2)點P在拋物線上運動,當點P運動到什么位置時△OAP的面積為2,請求出點P的坐標;
(3)在拋物線上是否存在一點Q,使△AFQ是等腰直角三角形?若存在直接寫出點Q的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《代數學》中記載,形如x2+10x=39的方程,求正數解的幾何方法是:“如圖1,先構造一個面積為x2的正方形,再以正方形的邊長為一邊向外構造四個面積為![]() x的矩形,得到大正方形的面積為39+25=64,則該方程的正數解為8-5=3”,小聰按此方法解關于x的方程x2+6x+m=0時,構造出如圖2所示的圖形,己知陰影部分的面積為36,則該方程的正數解為( )
x的矩形,得到大正方形的面積為39+25=64,則該方程的正數解為8-5=3”,小聰按此方法解關于x的方程x2+6x+m=0時,構造出如圖2所示的圖形,己知陰影部分的面積為36,則該方程的正數解為( )

A.6B.3![]() -3C.3
-3C.3![]() -2D.3
-2D.3![]() -
-![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,線段AB=CD,AB與CD相交于點O,且∠AOC=60°,CE是由AB平移所得,AC與BD不平行,則AC+BD與AB的大小關系是:AC+BD_____AB.(填“>”“<”或“=”)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人進行比賽的路程與時間的關系如圖所示.
(1)這是一場________米比賽;
(2)前一半賽程內________的速度較快,最終________贏得了比賽;
(3)兩人第________秒在途中相遇,相遇時距終點________米;
(4)甲在前8秒的平均速度是多少?甲在整個賽程的平均速度是多少?乙在前8秒的平均速度是多少?乙在整個賽程的平均速度是多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
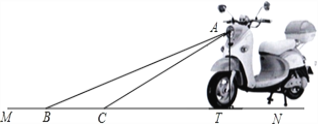
【題目】為響應國家的“節能減排”政策,某廠家開發了一種新型的電動車,如圖,它的大燈A射出的光線AB、AC與地面MN的夾角分別為22°和31°,AT⊥MN,垂足為T,大燈照亮地面的寬度BC的長為![]() m.
m.
(1)求BT的長(不考慮其他因素).
(2)一般正常人從發現危險到做出剎車動作的反應時間是0.2s,從發現危險到電動車完全停下所行駛的距離叫做最小安全距離.某人以20km/h的速度駕駛該車,從做出剎車動作到電動車停止的剎車距離是![]() ,請判斷該車大燈的設計是否能滿足最小安全距離的要求(大燈與前輪前端間水平距離忽略不計),并說明理由.
,請判斷該車大燈的設計是否能滿足最小安全距離的要求(大燈與前輪前端間水平距離忽略不計),并說明理由.
(參考數據:sin22°≈![]() ,tan22°≈
,tan22°≈![]() ,sin31°≈
,sin31°≈![]() ,tan31°≈
,tan31°≈![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線![]() 分別交x軸、y軸于A、B兩點,拋物線
分別交x軸、y軸于A、B兩點,拋物線![]() 經過A、B兩點,點C是拋物線與x軸的另一個交點(與A點不重合).
經過A、B兩點,點C是拋物線與x軸的另一個交點(與A點不重合).
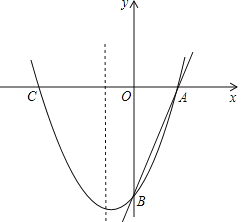
(1)求拋物線的解析式;
(2)求△ABC的面積;
(3)在拋物線的對稱軸上,是否存在點M,使△ABM為等腰三角形?若不存在,請說明理由;若存在,求出點M的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com