
【題目】在平面直角坐標系中,拋物線過原點O,且與![]() 軸交于另一點
軸交于另一點![]() ,其頂點為
,其頂點為![]() .孔明同學用一把寬為
.孔明同學用一把寬為![]() 帶刻度的矩形直尺對拋物線進行如下測量:
帶刻度的矩形直尺對拋物線進行如下測量:
① 量得![]() ;② 把直尺的左邊與拋物線的對稱軸重合,使得直尺左下端點與拋物線的頂點重合(如圖1),測得拋物線與直尺右邊的交點
;② 把直尺的左邊與拋物線的對稱軸重合,使得直尺左下端點與拋物線的頂點重合(如圖1),測得拋物線與直尺右邊的交點![]() 的刻度讀數為
的刻度讀數為![]() .
.
請完成下列問題:
(1)寫出拋物線的對稱軸;(2)求拋物線的解析式;(3)將圖中的直尺(足夠長)沿水平方向向右平移到點![]() 的右邊(如圖2),直尺的兩邊交
的右邊(如圖2),直尺的兩邊交![]() 軸于點
軸于點![]() 、
、![]() ,交拋物線于點
,交拋物線于點![]() 、
、![]() .求證:
.求證: ![]() .
.
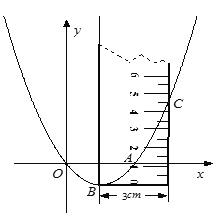
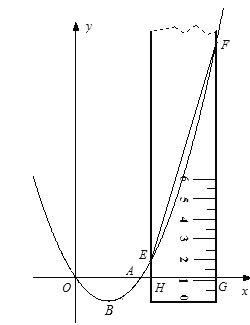
圖1 圖2
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】試題分析:(1)由于O、A關于拋物線對稱軸對稱,且OA=3cm,由此可求得拋物線的對稱軸為x=![]() .
.
(2)根據O、A的坐標,可將拋物線解析式設為交點式,在(1)題求得了拋物線的對稱軸,即可得到B、C的橫坐標,分別代入拋物線的解析式中,表示出它們的縱坐標,根據C、B的縱坐標差為4.5即可列方程求出待定系數的值,從而確定拋物線的解析式.
(3)可設出E點的橫坐標,進而根據直尺的寬度得到F點的橫坐標,根據(2)題所得拋物線,即可表示出兩點的縱坐標,利用梯形的面積公式,可求出梯形EFGH的面積表達式,然后同![]() (EF2-9)進行比較即可.
(EF2-9)進行比較即可.
試題解析:(1)![]()
(2)設拋物線的解析式為: ![]() ,當
,當![]() 時,
時, ![]() ,即
,即![]() ;當
;當![]() 時,
時, ![]() ,即
,即![]() ,依題意得:
,依題意得: ![]() ,解得:
,解得: ![]() .
.
∴拋物線的解析式為: ![]() .
.
(3)過點![]() 作
作![]() ,垂足為
,垂足為![]() ,設
,設![]() ,
, ![]() ,得:
,得: ![]() ①
①
![]() ②
②
又![]() ,得
,得 ,分別代入①、②得:
,分別代入①、②得: ![]() ,
, ![]()
∴![]() 得:
得: ![]()
又![]() ∴
∴![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,在所給正方形網格圖中完成下列各題:(用直尺畫圖,保留痕跡) 
(1)畫出格點△ABC(頂點均在格點上)關于直線DE對稱的△A1B1C1;
(2)在DE上畫出點Q,使△QAB的周長最小.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠CAB=∠DAB,則添加下列一個條件不能使△ABC≌△ABD的是( ) 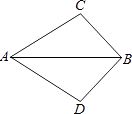
A.AC=AD
B.BC=BD
C.∠C=∠D
D.∠ABC=∠ABD
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲地宏達物流公司的快遞車和貨車同時從甲地出發,以各自的速度沿快速通道向乙地勻速行駛, 快遞車到達乙地后,卸完物資并另裝貨物共用了 45 分鐘,然后按原路以另一速度返回,直至與貨車相遇.已知貨車行駛速度為 60 km/h,兩車間的距離 y(km) 與貨車行駛時間 x(h) 之間的函數圖象如圖所示:
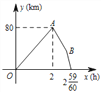
給出以下四個結論:
① 快遞車從甲地到乙地的速度是 100 km/h;
② 甲、乙兩地之間的距離是 80 km;
③ 圖中點 B 的坐標為 (![]() , 35);
, 35);
④ 快遞車從乙地返回時的速度為 90 km/h.
其中正確的是_____(填序號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角梯形ABCD中,AB∥DC,∠D=90o,AC⊥BC,AB=10![]() ,BC=6
,BC=6![]() ,F點以2
,F點以2![]() /
/![]() 的速度在線段AB上由A向B勻速運動,E點同時以1
的速度在線段AB上由A向B勻速運動,E點同時以1![]() /
/![]() 的速度在線段BC上由B向C勻速運動,設運動時間為
的速度在線段BC上由B向C勻速運動,設運動時間為![]() 秒(0<
秒(0<![]() <5).
<5).
(1)求證:△ACD∽△BAC; (2)求DC的長;
(3)設四邊形AFEC的面積為![]() ,求
,求![]() 關于
關于![]() 的函數關系式,并求出
的函數關系式,并求出![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綿陽市“全國文明村”江油白玉村果農王燦收獲枇杷20 t,桃子12 t.現計劃租用甲、乙兩種貨車共8輛將這批水果全部運往外地銷售,已知一輛甲種貨車可裝枇杷4 t和桃子1 t,一輛乙種貨車可裝枇杷和桃子各2 t.
(1)王燦如何安排甲、乙兩種貨車可一次性運到銷售地?有幾種方案?
(2)若甲種貨車每輛要付運輸費300元,乙種貨車每輛要付運輸費240元,則果農王燦應選擇哪種方案,使運輸費最少?最少運費是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A.擲一枚硬幣,正面一定朝上
B.某種彩票中獎概率為1%,是指買100張彩票一定有1張中獎
C.旅客上飛機前的安檢應采用抽樣調查
D.方差越大,數據的波動越大
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com