【題目】△ABC的內切圓的三個切點分別為D、E、F，∠A=75°，∠B=45°，則圓心角∠EOF=度．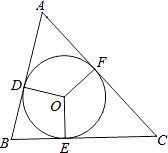 
【答案】120
【解析】解：∵∠A=75°，∠B=45°，
∴∠C=180°﹣75°﹣45°
=105°﹣45°
=60°
∵△ABC的內切圓的三個切點分別為D、E、F，
∴∠OEC=∠OFC=90°，
∵四邊形OECF的內角和等于360°，
∴∠EOF=360°﹣（90°+90°+60°）
=360°﹣240°
=120°
故答案為：120．
首先根據∠A=75°，∠B=45°，求出∠C=60°；然后根據△ABC的內切圓的三個切點分別為D、E、F，可得∠OEC=∠OFC=90°，再根據四邊形OEFC的內角和等于360°，求出圓心角∠EOF的度數是多少即可．此題主要考查了三角形的內切圓與內心，要熟練掌握，解答此題的關鍵是要明確：三角形的內心到三角形三邊的距離相等；三角形的內心與三角形頂點的連線平分這個內角．
優等生題庫系列答案
53天天練系列答案科目：初中數學 來源： 題型：
【題目】如圖，已知點E、F在四邊形ABCD的對角線BD所在的直線上，且BE=DF，AE∥CF，請再添加一個條件（不要在圖中再增加其它線段和字母），能證明四邊形ABCD是平行四邊形，并證明你的想法.
你所添加的條件：____________________________________；
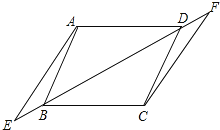
證明：
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】數學課上，張老師舉了下面的例題：
例1 等腰三角形
中，
，求
的度數.（答案：
）
例2 等腰三角形中，
，求的度數.（答案：
或
或
）
張老師啟發同學們進行變式，小敏編了如下一題：
變式 等腰三角形中，
，求的度數.
（1）請你解答以上的變式題.
（2）解（1）后，小敏發現，
的度數不同，得到的度數的個數也可能不同.如果在等腰三角形中，設
，當有三個不同的度數時，請你探索
的取值范圍.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】自學下面材料后，解答問題.
分母中含有未知數的不等式叫分式不等式.如：
；
等.那么如何求出它們的解集呢？根據我們學過的有理數除法法則可知：兩數相除，同號得正，異號得負.其字母表達式為：
(1)若
＞0，
＞0，則
＞0；若＜0，＜0，則＞0；
(2)若＞0，＜0，則＜0；若＜0，＞0，則＜0.
反之：(1)若＞0，則
或
(2)若＜0，則__________或__________.
(3)根據上述規律，求不等式
的解集.
(4)試求不等式
的解集.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知點P是△ABC內一點，且它到三角形的三個頂點距離之和最小，則P點叫△ABC的費馬點（Fermat point）．已經證明：在三個內角均小于120°的△ABC中，當∠APB=∠APC=∠BPC=120°時，P就是△ABC的費馬點．若點P是腰長為 
的等腰直角三角形DEF的費馬點，則PD+PE+PF= ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知二次函數y=x2﹣（2k+1）x+k2+k（k＞0）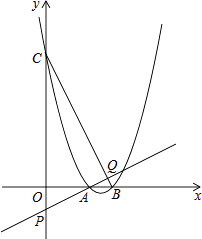
（1）當k= 
時，求這個二次函數的頂點坐標；
（2）求證：關于x的一元次方程x2﹣（2k+1）x+k2+k=0有兩個不相等的實數根；
（3）如圖，該二次函數與x軸交于A、B兩點（A點在B點的左側），與y軸交于C點，P是y軸負半軸上一點，且OP=1，直線AP交BC于點Q，求證： 
．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在數學活動課上，小明提出這樣一個問題：∠B=∠C=90°，E是BC的中點，DE平分∠ADC，如圖．大家一起熱烈地討論交流，小英第一個得出如下結論：（1）AE平分∠DAB；（2）△EBA≌△DCE；（3）AB+CD=AD；（4）AE⊥DE；（5）AB∥CD．其中正確的結論是_____．（將你認為正確結論的序號都填上）
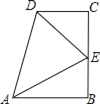
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如果一個三角形有一條邊上的高等于這條邊的一半，那么我們把這個三角形叫做半高三角形．已知直角三角形
是半高三角形，且斜邊
，則它的周長等于_________．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
