
【題目】如圖,為測量瀑布![]() 的高度,測量人員在瀑布對面山上的
的高度,測量人員在瀑布對面山上的![]() 點處測得瀑布頂端
點處測得瀑布頂端![]() 點的仰角是
點的仰角是![]() ,測得瀑布底端
,測得瀑布底端![]() 點的俯角是
點的俯角是![]() ,
,![]() 與水平面垂直.又在瀑布下的水平面測得
與水平面垂直.又在瀑布下的水平面測得![]() ,
,![]() (注:
(注:![]() 、
、![]() 、
、![]() 三點在同一直線上,
三點在同一直線上,![]() 于點
于點![]() ),斜坡
),斜坡![]() ,坡角
,坡角![]() ,那么瀑布
,那么瀑布![]() 的高度約為( ).(精確到
的高度約為( ).(精確到![]() ,參考數據:
,參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
A.![]()
![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
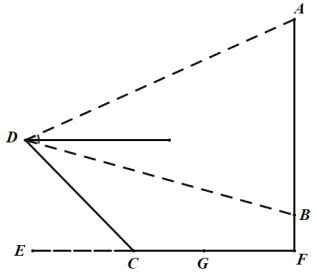
如圖,作DM⊥AB于M,DN⊥EF于N,在Rt△DCN中,求出CN即可得到FN的長,由四邊形DMFN是矩形可得DM的長,然后分別在Rt△ADM和Rt△DMB中,解直角三角形求出AM,BM即可解決問題.
解:如圖,作DM⊥AB于M,DN⊥EF于N,
在Rt△DCN中,CN=CDcos40°≈20.0×0.77=15.4(米),
∵CF=CG+GF=44.6(米),
∴FN=CN+CF=60.0(米),
易得四邊形DMFN是矩形,
∴DM=FN=60.0(米),
在Rt△ADM中,AM=DMtan30°=![]() (米),
(米),
在Rt△DMB中,BM=DMtan10°≈60.0×0.18=10.8(米),
∴AB=AM+BM=45.4(米),即瀑布![]() 的高度約為45.4米,
的高度約為45.4米,
故選:B.


科目:初中數學 來源: 題型:
【題目】定義:若兩條拋物線在x軸上經過兩個相同點,那么我們稱這兩條拋物線是“同交點拋物線”,在x軸上經過的兩個相同點稱為“同交點”,已知拋物線y=x2+bx+c經過(﹣2,0)、(﹣4,0),且一條與它是“同交點拋物線”的拋物線y=ax2+ex+f經過點(﹣3,3).
(1)求b、c及a的值;
(2)已知拋物線y=﹣x2+2x+3與拋物線yn=![]() x2﹣
x2﹣![]() x﹣n(n為正整數)
x﹣n(n為正整數)
①拋物線y和拋物線yn是不是“同交點拋物線”?若是,請求出它們的“同交點”,并寫出它們一條相同的圖像性質;若不是,請說明理由.
②當直線y=![]() x+m與拋物線y、yn,相交共有4個交點時,求m的取值范圍.
x+m與拋物線y、yn,相交共有4個交點時,求m的取值范圍.
③若直線y=k(k<0)與拋物線y=﹣x2+2x+3與拋物線yn =![]() x2﹣
x2﹣![]() x﹣n (n為正整數)共有4個交點,從左至右依次標記為點A、點B、點C、點D,當AB=BC=CD時,求出k、n之間的關系式
x﹣n (n為正整數)共有4個交點,從左至右依次標記為點A、點B、點C、點D,當AB=BC=CD時,求出k、n之間的關系式
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小元步行從家去火車站,走到 6 分鐘時,以同樣的速度回家取物品,然后從家乘出租車趕往火車站,結果比預計步行時間提前了3 分鐘.小元離家路程S(米)與時間t(分鐘)之間的函數圖象如圖,從家到火車站路程是( )
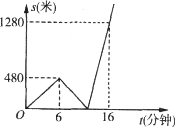
A.1300 米B.1400 米C.1600 米D.1500 米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中(如圖),已知函數
中(如圖),已知函數![]() 的圖像和反比例函數的在第一象限交于A點,其中點A的橫坐標是1.
的圖像和反比例函數的在第一象限交于A點,其中點A的橫坐標是1.
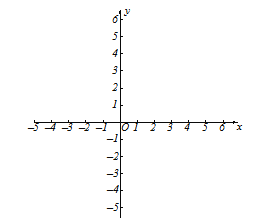
(1)求反比例函數的解析式;
(2)把直線![]() 平移后與
平移后與![]() 軸相交于點B,且
軸相交于點B,且![]() ,求平移后直線的解析式.
,求平移后直線的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某區正在積極創建國家模范衛生城市,學校為了普及學生衛生健康知識,提高學生創衛意識,舉辦了創衛知識競賽,以下是從初一、初二兩個年級隨機抽取20名同學的測試成績進行調查分析,成績如下:
初一:75 88 93 65 78 94 89 68 95 50 89 88 89 89 77 95 87 88 92 91
初二:74 96 96 89 97 74 69 76 72 78 99 72 97 85 98 74 89 73 98 74
(1)整理、描述數據:
成績 |
|
|
|
|
|
初一(頻數) | 1 | 2 | 3 |
| 6 |
初二(頻數) | 0 | 1 | 9 | 3 | 7 |
(說明:成績90分及以上為優秀,80~90分為良好,60~80分為合格,60分以下不合格)
分析數據:
平均數 | 中位數 | 眾數 | |
初一 | 84 |
| 89 |
初二 | 84 | 81.5 |
|
請根據上述的數據,填空:![]() ______;
______;![]() ______;
______;![]() ______;
______;
(2)得出結論:
你認為哪個年級掌握創衛知識水平較好并說明理由.(至少從兩個不同的角度說明推斷的合理性).
查看答案和解析>>
科目:初中數學 來源: 題型:
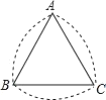
【題目】如圖所示的曲邊三角形可按下述方法作出:作等邊三角形![]() ;分別以點
;分別以點![]() ,
,![]() ,
,![]() 為圓心,以
為圓心,以![]() 的長為半徑作
的長為半徑作![]() ,
,![]() ,
,![]() .三段弧所圍成的圖形就是一個曲邊三角形,如果一個曲邊三角形的周長為
.三段弧所圍成的圖形就是一個曲邊三角形,如果一個曲邊三角形的周長為![]() ,那么這個曲邊三角形的面積是___________.
,那么這個曲邊三角形的面積是___________.
查看答案和解析>>
科目:初中數學 來源: 題型:
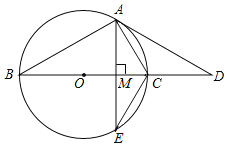
【題目】已知BC是⊙O的直徑,點D是BC延長線上一點,AB=AD,AE是⊙O的弦,∠AEC=30°.
(1)求證:直線AD是⊙O的切線;
(2)若AE⊥BC,垂足為M,⊙O的半徑為4,求AE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,長方形ABCD中,AD∥BC,∠B=90°,AD=BC=20,AB=8,動點P從點B出發,先以每秒2cm的速度沿B→A的方向運動,到達點A后再以每秒4cm的速度沿A→D的方向向終點D運動;動點Q從點B出發以每秒2cm的速度沿B→C的方向向終點C運動.其中一個動點到達終點時,另一個動點也隨之停止運動,設點P、Q同時出發,運動時間為t秒.
(1)直接寫出BQ的長(用含t的代數式表示)
(2)求△BPQ的面積S(用含t的代數式表示)
(3)求當四邊形APCQ為平行四邊形t的值
(4)若點E為BC中點,直接寫出當△BEP為等腰三角形時t的值.
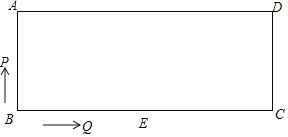
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com